Анализ электронных схем
Евгений Мисник
15 апреля 2019 г.

Данная статья предназначена для возможноти ознакомления с машин-
ным расчётом электронных схем. Здесь описываются правила расчёта, ал-
горитмы решения систем линейных уравнений, знакомство с матрицами.
Статья может быть интересна учащимся школ или средних технических
заведений в качестве ознакомительного курса.
Издание второе, переработанное.
i

ii
Оглавление
1 Линейные цепи постоянного тока 3
1.1 Линейные двухполюсники . . . . . . . . . . . . . . . . . . . . . 3
1.2 Линейные многополюсники . . . . . . . . . . . . . . . . . . . . 4
2 Модели компонентов 5
2.1 Источник напряжения . . . . . . . . . . . . . . . . . . . . . . . 5
2.2 Источник тока . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.3 Преобразование I ⇒ U . . . . . . . . . . . . . . . . . . . . . . . 6
2.4 Элементы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.5 Динамический анализ линейных цепей . . . . . . . . . . . . . . 10
2.5.1 Анализ во времени . . . . . . . . . . . . . . . . . . . . . 11
2.5.2 Метод Эйлера . . . . . . . . . . . . . . . . . . . . . . . . 12
2.6 Статический анализ нелинейных цепей . . . . . . . . . . . . . 15
2.6.1 Решение проблемы . . . . . . . . . . . . . . . . . . . . . 15
2.6.2 Алгоритм Ньютона-Рафсона . . . . . . . . . . . . . . . . 16
2.7 Диод . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.7.1 Нелинейный двухполюсник . . . . . . . . . . . . . . . . 19
2.7.2 Расширенная модель диода . . . . . . . . . . . . . . . . 20
2.8 Транзистор . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
3 Системы линейных уравнений 25
3.1 Алгоритм Гаусса . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.2 Другие методы . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
4 Приложение 29
4.1 Основы операций с матрицами . . . . . . . . . . . . . . . . . . 29
4.1.1 Матрицы и детерминанты . . . . . . . . . . . . . . . . . 29
4.1.2 Сложение и вычитание . . . . . . . . . . . . . . . . . . . 30
4.1.3 Умножение . . . . . . . . . . . . . . . . . . . . . . . . . 30
4.2 Основы теории графов . . . . . . . . . . . . . . . . . . . . . . . 30
4.2.1 Основные понятия . . . . . . . . . . . . . . . . . . . . . 30
4.2.2 Решение графа . . . . . . . . . . . . . . . . . . . . . . . 31
4.2.3 Правила преобразования графов . . . . . . . . . . . . . 31
4.2.4 Примеры с графами . . . . . . . . . . . . . . . . . . . . 33
4.3 Законы Кирхгофа . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4.3.1 Метод узловых потенциалов . . . . . . . . . . . . . . . . 36
4.3.2 Метод контурных токов . . . . . . . . . . . . . . . . . . 36
4.4 Примеры описания электрических схем . . . . . . . . . . . . . 37
iii

ОГЛАВЛЕНИЕ
4.4.1 Пример схемы с резисторами . . . . . . . . . . . . . . . 37
4.4.2 Пример с использованием источников тока, управляе-
мых напряжением . . . . . . . . . . . . . . . . . . . . . . 38
4.4.3 Пример о операционным усилителем . . . . . . . . . . . 39
4.5 Листинги программ . . . . . . . . . . . . . . . . . . . . . . . . . 40
4.5.1 Гаусс . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
iv
Список иллюстраций
1.1 Пример цепи постоянного тока . . . . . . . . . . . . . . . . . . 3
2.1 Идеальный источник напряжения . . . . . . . . . . . . . . . . . 5
2.2 Реальный источник напряжения . . . . . . . . . . . . . . . . . 5
2.3 Идеальный источник тока . . . . . . . . . . . . . . . . . . . . . 6
2.4 Реальный источник тока . . . . . . . . . . . . . . . . . . . . . . 6
2.5 Преобразование источника напряжения в источник тока . . . 6
2.6 Схема замещения малосигнального транзистора . . . . . . . . 10
2.7 Замещение операционного усилителя . . . . . . . . . . . . . . . 10
2.8 Включение ёмкости . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.9 Определение тангенса угла наклона кривой в методе Эйлера . 12
2.10 Дискретная токовая модель ёмкости в неявном методе Эйлера 13
2.11 Схема замещения индуктивности и дискретная токовая мо-
дель для интуктивности, используемая в неявном методе Эй-
лера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.12 Пример
нелинейной цепи . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.13 Принцип итераций Ньютона-Рафсона . . . . . . . . . . . . . . 16
2.14 Касательная к функции . . . . . . . . . . . . . . . . . . . . . . 17
2.15 Диод . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.16 Вольт-амперная характеристика диода . . . . . . . . . . . . . . 18
2.17 Схема замещения нелинейного двухполюсника . . . . . . . . . 19
2.18 Матрица проводимостей и векторных токов нелинейного двух-
полюсника . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
2.19 Малосигнальная модель диода на средних частотах . . . . . . 20
2.20 Более общая модель диода . . . . . . . . . . . . . . . . . . . . . 20
2.21 Биполярные транзисторы . . . . . . . . . . . . . . . . . . . . . 21
2.22 Упрощённая конструкция транзистора . . . . . . . . . . . . . . 22
2.23 Т-образная схема замещения транзистора . . . . . . . . . . . . 22
2.24 Модель Эберса-Молла . . . . . . . . . . . . . . . . . . . . . . . 23
4.1 Сложение с исключением ветви . . . . . . . . . . . . . . . . . . 32
4.2 Умножение с исключением узла . . . . . . . . . . . . . . . . . . 32
4.3 Исключение петли . . . . . . . . . . . . . . . . . . . . . . . . . . 33
4.4 Граф схемы (рис.4.7). . . . . . . . . . . . . . . . . . . . . . . . . 34
4.5 ОУ и его граф . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
4.6 Усилитель на ОУ . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4.7 Контурные токи . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
v

СПИСОК ИЛЛЮСТРАЦИЙ
4.8 Пример схемы с описанием . . . . . . . . . . . . . . . . . . . . . 37
4.9 Схема транзисторного усилителя . . . . . . . . . . . . . . . . . 38
4.10 Схема замещения транзисторного усилителя . . . . . . . . . . 39
4.11 Инвентирующий операционный усилитель . . . . . . . . . . . . 39
vi
Список таблиц
2.1 Построение системы линейных двухполюсников . . . . . . . . 7
2.2 Пример таблицы элементов . . . . . . . . . . . . . . . . . . . . 8
2.4 Источник тока, управляемый напряжением . . . . . . . . . . . 8
2.3 Таблица моделей мсточников сигналов . . . . . . . . . . . . . . 9
2.5 Ёмкость в системе узловых потенциалов . . . . . . . . . . . . . 14
2.6 Матрица узловых напряжений и токов для n−p−n транзистора 24
1

СПИСОК ТАБЛИЦ
2
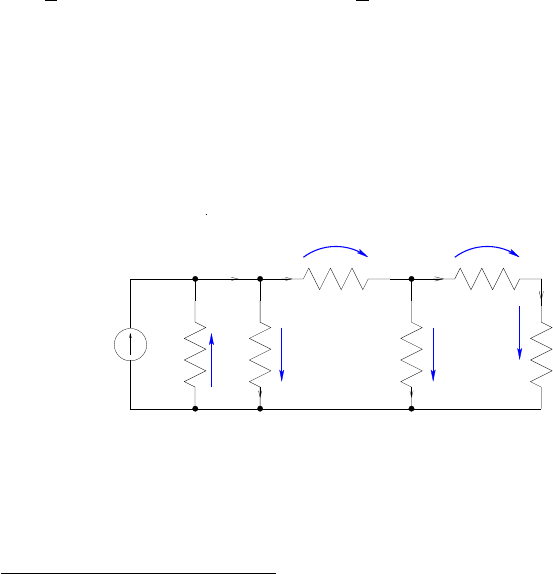
Глава 1
Линейные цепи постоянного
тока
1.1 Линейные двухполюсники
Линейными двухполюсными цепями называют цепи, содержащие только
такие двухполюсниками, вольт-амперная характеристика (ВАХ) которых
есть прямая линия. Для постоянного тока - это активное сопротивление
R =
U
I
= const или проводимость G =
I
U
= const,
где U = const - идеальный источник напряжения и I = const - идеальный
источик тока.
Цепи, содержащие такие двухполюсные элементы, называют линейными.
Ниже приводится пример цепи постоянного тока с шестью ветвями
1
и
тремя узлами
2
:
g6
u4
(1) (2)
(0)
(3)
u1 u2
i5
i6
u6
i2 i4
i1
i3
g1 g4g2
g3 g5
u3 u5
Рис. 1.1: Пример цепи постоянного тока
1
Ветвью называется участок цепи с последовательным соединением элементов.
2
Узлом в электрической цепи называеися место соединения трёх и более ветвей.
3

ГЛАВА 1. ЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Методом узловых потенциалов составим систему уравнений для выше-
приведённой цепи:
I
2
+ I
3
− I
1
= 0
I
4
+ I
5
− I
3
= 0
I
6
− I
5
= 0
(1.1)
Если заменить ток в каждой ветви, заменив I = U ∗ R, получим:
G
2
U
2
+ G
3
U
3
− G
1
U
1
− I
q
= 0
G
4
U
4
+ G
5
U
5
− G
3
U
3
= 0
G
6
U
6
− G
5
U
5
= 0
(1.2)
Напряжение в каждой ветви можно выразить через узловые напряже-
ния:
U
1
= −U
1,0
; U
2
= U
1,0
; U
3
= U
1,0
− U
2,0
; U
4
= U
2,0
; U
5
= U
2,0
− U
3,0
;
U
6
= U
3,0
.
Подставляя полученные выражения в узловые уравнения, получаем:
(G
1
+ G
2
+ G
3
)U
1,0
− G
3
U
2,0
= I
q
−G
3
U
1,0
+ (G
3
+ G
4
+ G
5
)U
2,0
− G
5
U
3,0
= 0
−G
5
U
2,0
+ (G
5
+ G
6
)U
3,0
= 0
(1.3)
Эту систему уравнений можно записать в матричной форме:
G
1
+ G
2
+ G
3
−G
3
−G
3
G
3
+ G
4
+ G
5
−G
5
−G
5
G
5
+ G
6
∗
U
1,0
U
2,0
U
3,0
=
I
q
0
0
(1.4)
Матрицу, содержащую проводимости, называют матрицей узловых про-
водимостей. Для двухполюсных цепей матрица симметрична. Структура
матрицы подчиняется определённым правилам[1]: в каждом элементе глав-
ной диагонали матрицы стоит сумма проводимостей, которые одним своим
полюсом соединены с соответствующим узлом. Во всех остальных элемен-
тах размещается отрицательная сумма тех проводимостей, которые распо-
ложены между узлами. Матрица с одним столбцом токов источников стро-
ится также согласно строгим правилам: ток I
q
источника получает отрица-
тельный знак для того узла, из которого он “выходит”, и положительный
для узла, в который он “входит”.
1.2 Линейные многополюсники
По определению четырёхполюсник представляет собой электрическую
цепь, в которой различают два входных и два выходных зажима.
4

Глава 2
Модели компонентов
2.1 Источник напряжения
Идеальный источник напря-
жения E, независимо от про-
текающего во внешней цепи
тока, имеет постоянное напря-
жение U = E = const.(рис.2.1)
Реальный источник напряже-
ния имеет внутреннее сопро-
тивление r
i
.(рис.2.2)
E
U
Рис. 2.1: Идеальный источник на-
пряжения
E
Ri
U
Рис. 2.2: Реальный источник на-
пряжения
2.2 Источник тока
Идеальный источник тока I, незави-
симо от нагрузки во внешней цепи,
выдаёт постоянный, неизменный ток
I = onst. (рис.2.3)
Реальный источник тока име-
ет внутреннюю проводимость
g
i
. (рис.2.4)
5
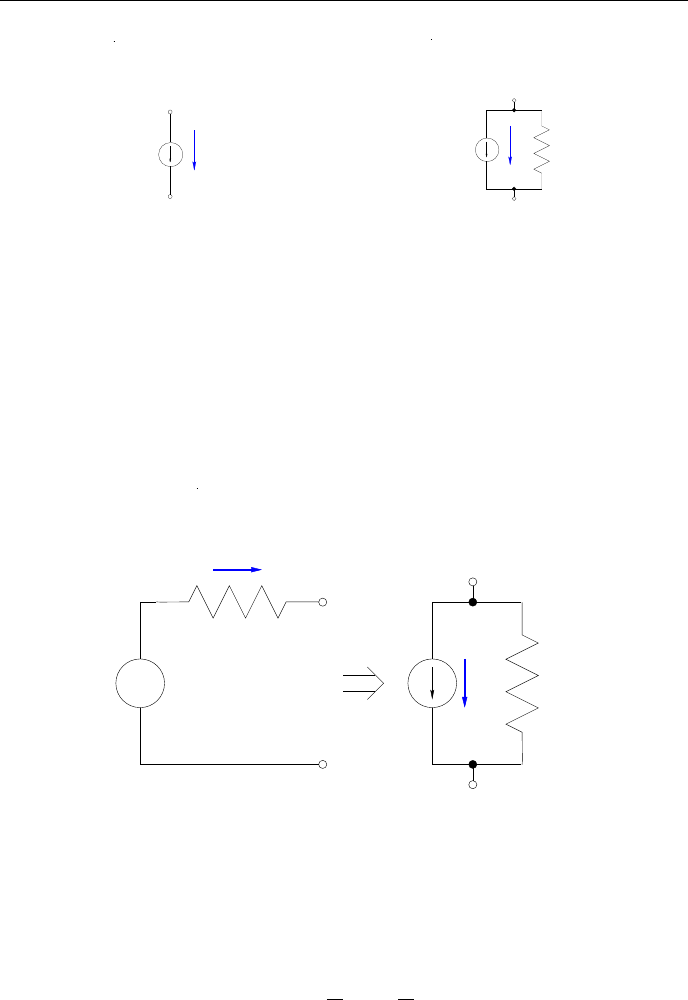
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
I
Рис. 2.3: Идеальный источник то-
ка
G
I
Рис. 2.4: Реальный источник тока
2.3 Преобразование I ⇒ U
Преобразование источника напряжения в источник тока показано на
следующем рисунке (рис.2.5):
+
−
E
U
Ri
I
Gi
I=E/R
G=1/R
Рис. 2.5: Преобразование источника напряжения в источник тока
Линейный источник напряжения может быть преобразован в линейный
источник тока следующим образом:
I = −
U
R
, G =
1
R
(2.1)
Преобразование идеального источника напряжения, у которого R = 0, в
линейный источник напряжения невозможно.
2.4 Элементы
Покажем на примере матрицу системы линейных уравнений для двух-
полюсников (таб.2.1):
6
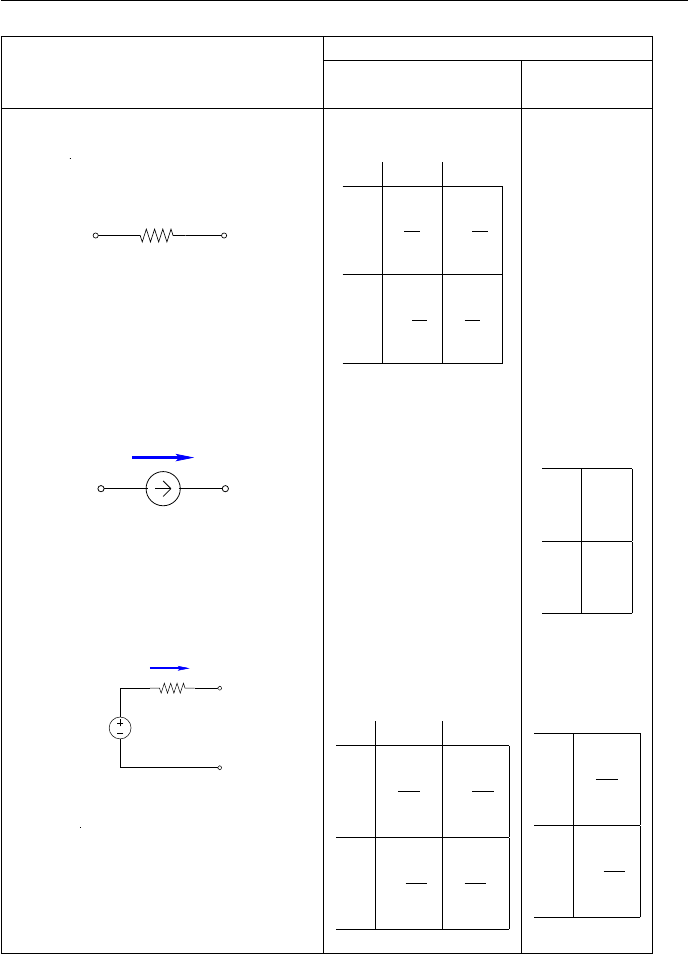
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
Система узлов
Матрица узловых Вектор
значений токов
Омическое сопротивление
X Y
X Y
X
1
R
−
1
R
Y
−
1
R
1
R
Источник постоянного тока
X Y
X I
Y −I
Реальный источник напряжения
E
Ri
X
Y
X Y
X
1
R
i
−
1
R
i
Y
−
1
R
i
1
R
i
X
E
R
i
Y
−
E
R
i
Таблица 2.1: Построение системы линейных двухполюсников
Ниже представлен пример таблицы массивов для некоторых элементов
электрических схем (таб.2.2):
Исходя из представленной таблицы видно, что не всем элементам нужна
такая размерность массива (отдельные ячейки пустые). Поэтому при же-
лании экономии памяти компьютера для каждого вида элементов можно
создать свою размерность массива.
7
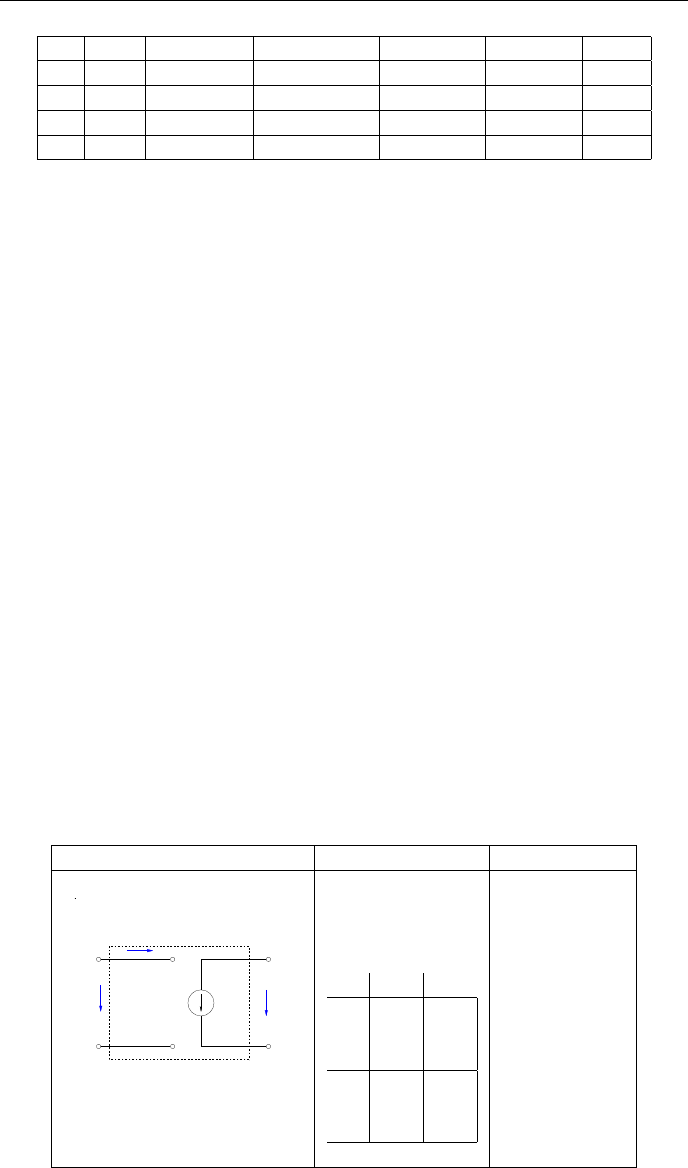
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
# Тип Значение Вн.Сопрот. Узел (+) Узел (-) Узел
R
i
10 2 0
C
i
100 1 2
E
i
0 12 0.001 1 0 I
i
Q
i
3 2 0 3
Для “типа” указываются типы элементов (тип источника напряжения или
сигнала, тип транзистора.
“Значение” для резисторов задаётся в kOm, конденсаторов - в pF, напряже-
ние - в V.
“Веутреннее сопротивление” для источника напряжения как и для резисто-
ров задаётся в kOm.
“Узел”. Узел (+) для источника напяжения или база для транзистора. Узел
(-) для источника напряжения и эмиттер для транзистора, а также узел
для коллектора транзистора.
Для источника напряжения одна из ячеек массива хранит значение тока
(см.2.1)
Таблица 2.2: Пример таблицы элементов
Также приводится возможная таблица моделей источников сигналов
(таб.2.3):
Рассмотрим ещё один из типов линейных элементов - управляемый ис-
точник. Для расчёта активного четырёхполюсника исходят из принципа
замещения линейными двухполюсниками, после чего расчитывается как
схема из двухполюсников.
Каждый линейный активный четырёхполюсник может быть заменён ли-
нейным управляемым источником тока или напряжения. В качестве управ-
ляющего параметра используется ток или напряжение ветви, причём управ-
ляемая ветвь является либо источником тока, либо источником напряже-
ния.
Источник тока, управляемый напряжением (ИТУН).
ИТУН Матрица узлов Вектор токов
SU
2
U
2
U
1
L
M
I
1
J
K
J K
L −S S
M S −S
Таблица 2.4: Источник тока, управляемый напряжением
8

ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
Тип Обозначение Осциллограмма Определения
0 Постоянный
6
x
- t
0
X
x
t
= X
1 Единичный
6
x
- t
0
X
x
t
=
(
0 для t < 0
X для t > 0
2 Выключение
6
x
- t
0
X
x
t
=
(
X для t ≤ 0
0 для t > 0
3 Нарастающий
6
x
- t
0
X
x
t
= Xt
4 Синус
6
x
- t
0
X
−X
-
T
x
t
= X sin
2π
T
0
t
5 Меандр (1)
6
x
- t
0
X
-
T
x
t
=
(
X для sin
2π
T
o
t > 0
0
6 Меандр (2)
6
x
- t
0
X
−X
-
T
x
t
=
(
X для sin
2π
T
0
t > 0
−X
7 Импульс
6
x
- t
0
X
-
T
x
t
=
(
X для 0 < t < T
0
0
Таблица 2.3: Таблица моделей мсточников сигналов
9
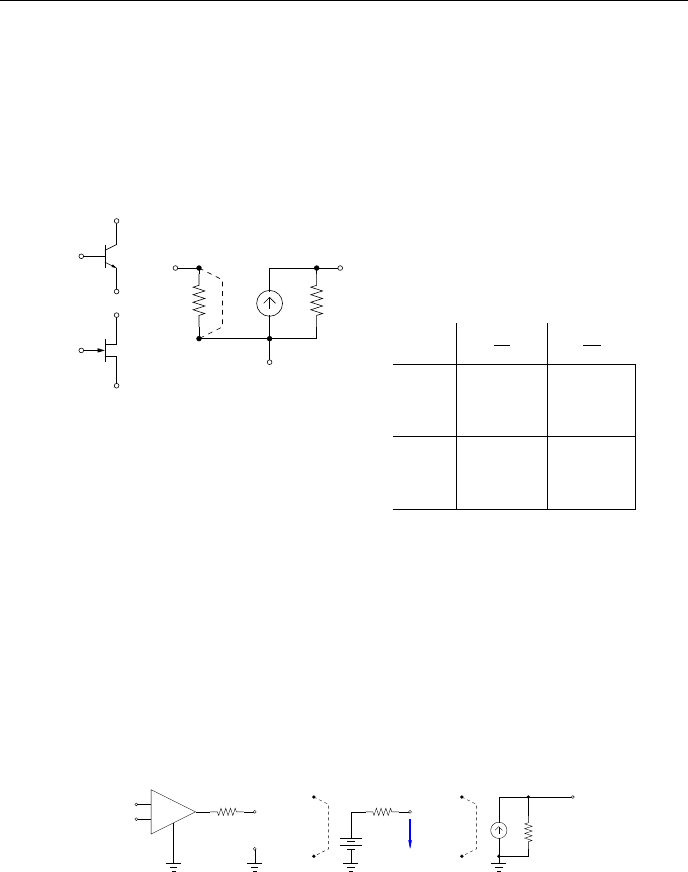
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
В качестве примера использования вышеупомянутого четырёхполюс-
ника можно рассмотреть схему замещения малосигнального транзистора
(рис.2.6).
Линейная статическая схема замещения транзистора и Y-матрица че-
тырёхполюсника:
+
−
E/S
B/G C/D
g g
11 22
S=g
21
B
C
E
G
S
D
B
G
C
D
B/G g
11
g
12
= 0
C/D g
21
= S g
22
Рис. 2.6: Схема замещения малосигнального транзистора
Ещё один пример - операционный усилитель.
Ue
Ua
Ra
k=Ua/Ue
E=−kUe
Ra
UaUe
+
−
+
−
Ue Ra
+
−
S=k/Ra
+
−
−
+
Рис. 2.7: Замещение операционного усилителя
2.5 Динамический анализ линейных цепей
В предыдущих главах рассматривались цепи в установившемся режиме,
когда все параметры постоянны во времени. Подобный режим работы назы-
10

ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
вается статическим, и считается, что временн´ая зависимость параметров
этих цепей известна.
Целью динамического анализа элекирических цепей является выяснение
изменяющегося т.е. зависящего от времени напряжения в узлах. Рассчиты-
ваются параметры цепи, структура которой изменяется в течение переход-
ного процесса. После подключения питания в момент t = 0 и до перехода в
установившийся режим параметры цепи меняются во времени до тех пор,
пока не примут окончательные значения. В этом переходном состоянии цепь
называется динамической.
Далее речь пойдёт о цепях с линейными двухполюсниками и управляе-
мыми источниками, коэффициент управления которых постоянен. Линей-
ными двухполюсниками являются базовые двухполюсники R, G, L и C и
идеальные источники, собственные параметры которых не зависят от на-
грузки.
При расчёте в структуру цепей вносятся некоторые ограничения. На-
пример, напряжение на зажимах идеального источника напряжения уже
задано. Поэтому двухполюсник, параметром состояния которого являет-
ся напряжение, может быть связан с идеальным источником напряжения
только в установившемся режиме.
2.5.1 Анализ во времени
Анализ переходного процесса
Если цепь содержит индуктивность L или ёмкость C,
то аналитически параметры цепи, зави-
+
−
Re
C
E
Ue
t=0
Ua
Рис. 2.8: Включение ёмкости
сящие от времени, можно рассчитать толь-
ко путём решения дифференциальных урав-
нений. На рис.2.8 показан пример цепи, в
которой ёмкость подключается к линейно-
му источнику постоянного напряжения. В
начальный момент времени t = 0 u
c
= u
a
.
При постоянной времени τ = R
e
C решение
выглядит так:
u
c
= U
e
+ (U
a
− U
e
) exp
−t
τ
. (2.2)
Аналитическое решение для переходных значений параметров динами-
ческой цепи можно получить и с помощью преобразования Лапласа.
Дискретизация по времени
При анализе переходных процессов определяются мгновенные значения
каждого параметра цепи для дискретных моментов времени. На основании
начальных условий (t = 0) вычисляются параметры цепи сначала в мо-
мент t
1
, затем в моменты t
2
, t
3
, . . . , t
e
. В конечный момент t
e
вычисления
прекращаются.
11
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
Каждый параметр вычисляется на основании значений, полученных в
предыдущие моменты времени.
2.5.2 Метод Эйлера
При анализе переходных процессов цепи с несколькими реактивными
элементами необходимо для каждого момента времени t
j+1
решить систе-
му обыкновенных дифференциальных уравнений. В качестве примера мож-
но рассмотреть дифференциальное уравнение первого порядка, которое со-
держит кроме переменной x ещё и производную первого порядка от этой
переменной
x
0
=
dx
dt
= λx. (2.3)
Для дискретного вычисления значения x
j+1
в момент времени t
j+1
необ-
ходимо определить производную
dx
dt
. Для этого можно воспользоваться ме-
тодом конечных приращений Эйлера.
6
-
x
t
x
j
t
j
x
j+1
t
j+1
#
#
#
#
#
#
Рис. 2.9: Определение тангенса угла наклона кривой в методе Эйлера
Функцию x(t) между точками t
j
и t
j+1
можно аппроксимировать прямой
линией (рис.2.9). Наклон прямой
dx
dt
=
x
j+1
− x
j
t
j+1
− t
j
=
x
j+1
− x
j
h
. (2.4)
Уравнение (2.4) описывает производную как в момент времени t
j
:
x
0
(t
j
) =
x
j−1
− x
j
h
, (2.5)
так и в момент времени t
j+1
:
x
0
(t
j+1
) =
x
j+1
− x
j
h
. (2.6)
12
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
При аппроксимации уравнение (2.5) примет вид:
x
j+1
= x
j
+ hx
0
(t
j
). (2.7)
Формула (2.7) известна как прямой метод Эйлера. Обратный метод Эй-
лера аналогичен прямому, но есть отличие в аппроксимации для производ-
ной (2.6). Такая аппроксимация даёт формулу обратного метода Эйлера:
x
j+1
= x
j
+ hx
0
(t
j+1
). (2.8)
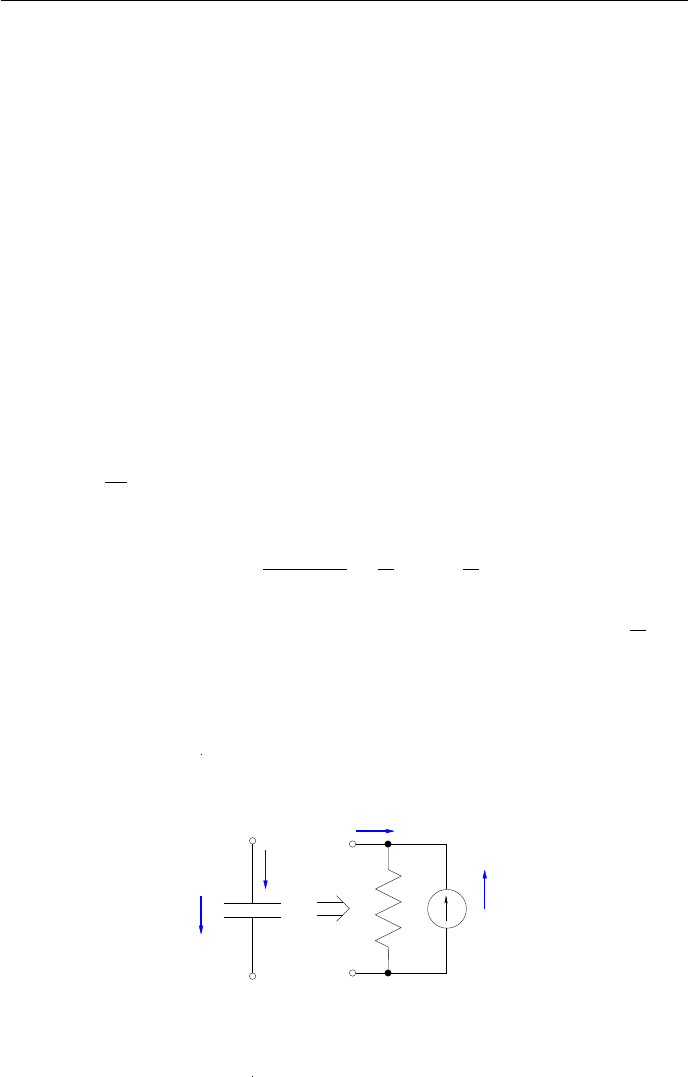
Интегрирование на уровне двухполюсников
Метод Эйлера можно использовать для цепей, содержащих ёмкости и
индуктивности.Для расчёта необходимы уравнения связи между последу-
ющими u
j+1
, i
j+1
и предыдущими u
j
, i
j
значениями напряжений и токов.
Составив уравнение связи для ёмкости с учётом уравнения двухполюс-
ника i = C
du
dt
(при C = const) рассчитываеися в соответствии с (2.4) ток,
протекающий в момент времени
i
j+1
= C
u
j+1
− u
j
h
=
C
h
u
j+1
−
C
h
u
j
. (2.9)
Первый член уравнения характеризует ток в проводимости G =
C
h
при
напряжении u
j+1
. Второй член уравнения можно интерпретировать как соб-
ственный ток идеального источника тока. Схема замещения для уравнения
(2.9) приведена на рис.2.10
Uc
Ic
Ic
t+1
C/h
(C/h)*Uc
t
Рис. 2.10: Дискретная токовая модель ёмкости в неявном методе Эйлера
Эту схему можно называть дискретной моделью токового контура (discrete
circuit model) [3].
13
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
При анализе электрических цепей с ёмкостями методом узловых потен-
циалов необходимо в ходе решения узловых уравнений вычислить напря-
жение ветви u
j+1
в момент t
j+1
. Затем определяется ток источника I
q
для
следующего шага вычислений.
Таблица для ёмкости в системе узловых потенциалов выглядит так:
Ёмкость Матрица узлов Вектор токов
C/h
(L)
(M)
(C/h)*U
LM
L M
L
C
h
−
C
h
M
−
C
h
C
h
L
C
h
U
LM
M
−
C
h
U
LM
Таблица 2.5: Ёмкость в системе узловых потенциалов
Попробуем сформировать дискретную модель токового контура для ин-
дуктовности L = const. С учётом уравнения двухполюсника u = L
di
dt
в
момент времени t
j+1
напряжение на нём будет равно
u
j+1
= L
i
j+1
− i
j
h
=
L
h
i
j+1
−
L
h
i
j
. (2.10)
Первый член в правой части уравнения характеризует падение напря-
жения, вызванное током i
j+1
в активном сопротивлении R =
L
h
, а второй
член может быть интерпретирован как собственное напряжение идеально-
го источника напряжения (рис.2.11). Чтобы использовать метод узловых
потенциалов для расчёта схемы на рис.2.11 , надо заменить линейный ис-
точник напряжения линейным источником тока, у которого
G =
1
R
=
h
L
, (2.11)
I
q
=
−u
q
R
= i
j
. (2.12)
Если методом узловых потенциалов анализируется цепь с индуктивно-
стью, то после вычисления узлового напряжения в момент t
j+1
определя-
ется напряжение в ветви u
j+1
, а затем ток
i
j+1
=
h
L
u
j+1
+ i
j
, (2.13)
являющиййся собственным током источника для дальнейших шагов вы-
числений.
14
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
R=(L/h)
Uq=−(L/h)*i
+
−
U
j+1
I
j+1
G=(h/L)
I
q
=i
j
U
j+1
I
j+1
L
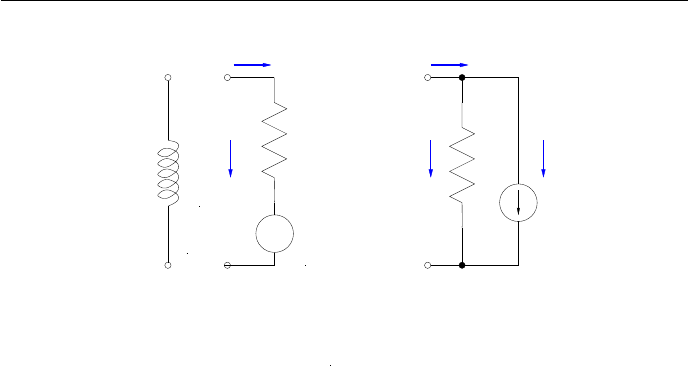
Рис. 2.11: Схема замещения индуктивности и дискретная токовая модель
для интуктивности, используемая в неявном методе Эйлера
2.6 Статический анализ нелинейных цепей
2.6.1 Решение проблемы
В практике часто встречаются электрические цепи, значения парамет-
ров отдельных элементов которых заметно изменяются с именением проте-
кающего через этот элемент тока. Эти элементы имеют нелинейные харак-
теристики и называются нелинейными элементами.
Строго говоря, большинство элементов электрических цепей постоян-
ного тока являются нелинейными, т. к. с изменением протекающего тока
изменяется температура элемента. Следовательно меняется и сопротивле-
ние этого элемента. В статической нелинейной цепи имеется как минимум
один элемент с нелинейной ВАХ (напр. диод).
Для анализа цепей реальные элементы можно заменить двухполюсни-
ками и управляемыми источниками, и такой процесс можно назвать моде-
лированием.
С помощью модели упрощённо описывается процесс или объект. Од-
нако, в ряде случаев, простая модель не отражает существенных свойств
реального процесса или объекта.
Отыскание рабочей точки или расчёт по постоянному току обычно яв-
ляется первым шагом при анализе нелинейных схем. Он включает в себя
определение узловых напряжений в схеме при данных параметрах источни-
ков постоянного тока и требует решения систем нелинейных алгебраических
уравнений.
Модели активных приборов обычно включают в себя экспоненциальные
функции, которые могут затруднять вычисления.
Во многих случаях нелинейные функции, содержащиеся в моделях дио-
дов и транзисторов, известны в виде таблиц, а не формул. В этой ситуации
возможна кусочная линеаризация между заданными точками. Алгоритм,
15
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
ориентированный на кусочно-линейные системы, был предложен Катце-
нельсоном [4].
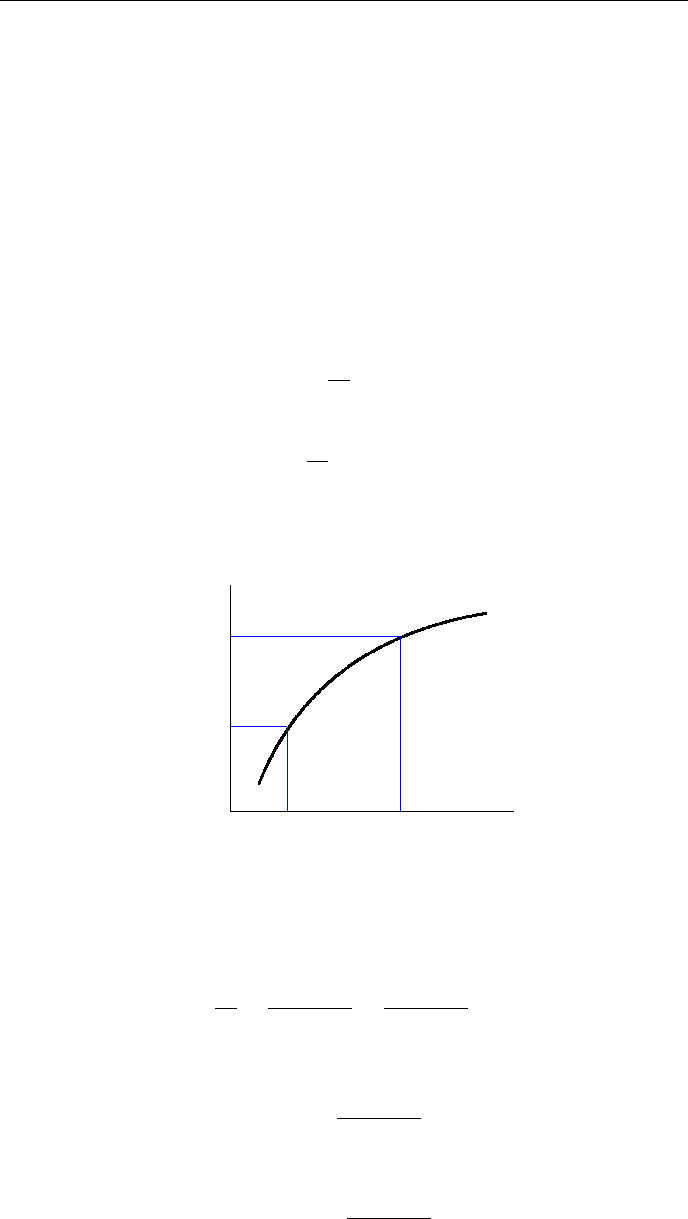
2.6.2 Алгоритм Ньютона-Рафсона
Алгоритм Ньютона-Рафсона был введён как один из методов отыска-
ния корней полиномов. Он хорошо известен, широко используется и имеет
квадратичную сходимость, если начальное приближение близко к точному
решению.
При решении уравнения f(x) = 0 в скалярном случае итерации Ньютона-
Рафсона опредеояется выражением
x
k+1
= x
k
+ ∆x
k
= x
k
−
f(x
k
)
f
0
(x
k
)
. (2.14)
Номер итерации указывается верхним индексом.
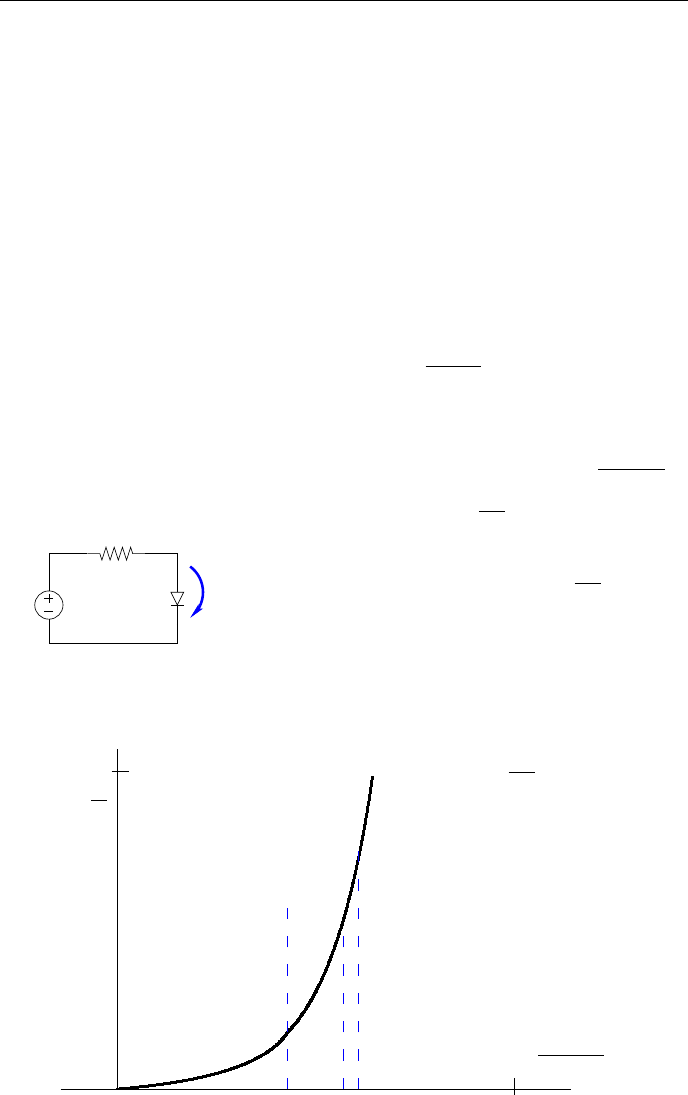
Рассмотрим пример простой нелинейной статической цепи (рис.2.12).
Из уравнений I
D
=
E − V
D
R
и
V
D
R
E
Рис. 2.12: Примернелинейной цепи
I
D
= I
s
(exp
V
D
V
T
− 1) получается
V
D
= E − RI
s
exp
V
D
V
T
− 1
.
(2.15)
Для решения уравнения можно
воспользоваться методом итераций.
Для этого можно рассмотреть прин-
цип итераций, показанный на рис.2.13.
-
6
0 V
D
I
D
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
c
I
D
=
E − V
D
R
E
R
E
I
D
= I
s
(exp
V
D
V
T
)
V
0
D
e
e
e
V
1
D
e
V
2
D
e
Рис. 2.13: Принцип итераций Ньютона-Рафсона
Рассмотрим графическое решение нахождения искомой точки. За основу
берутся два параметра: начальная точка V
0
D
и точность расчёта ε. Проводим
16
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
вертикальную черту из точки V
0
D
до пересечения с кривой характеристи-
ки диода. Через полученную точку пересечения проведём касательеую к
заданной кривой, которая в свою очередь пересечёт нагрузочную прямую
I
D
=
E − V
D
R
. Полученная точка V
1
D
будет следующей точкой итерации.
Через неё опять проведём вертикальную черту до пересечения с кривой.
Вновь через полученную точку пересечения проведём касательную к кри-
вой, которая в свою очередь пересечёт нагрузочную прямую. Следующий
шаг итерации повторяет ранее описанный, и так до тех пор, пока результат
ошибки будет меньше или равен ε.
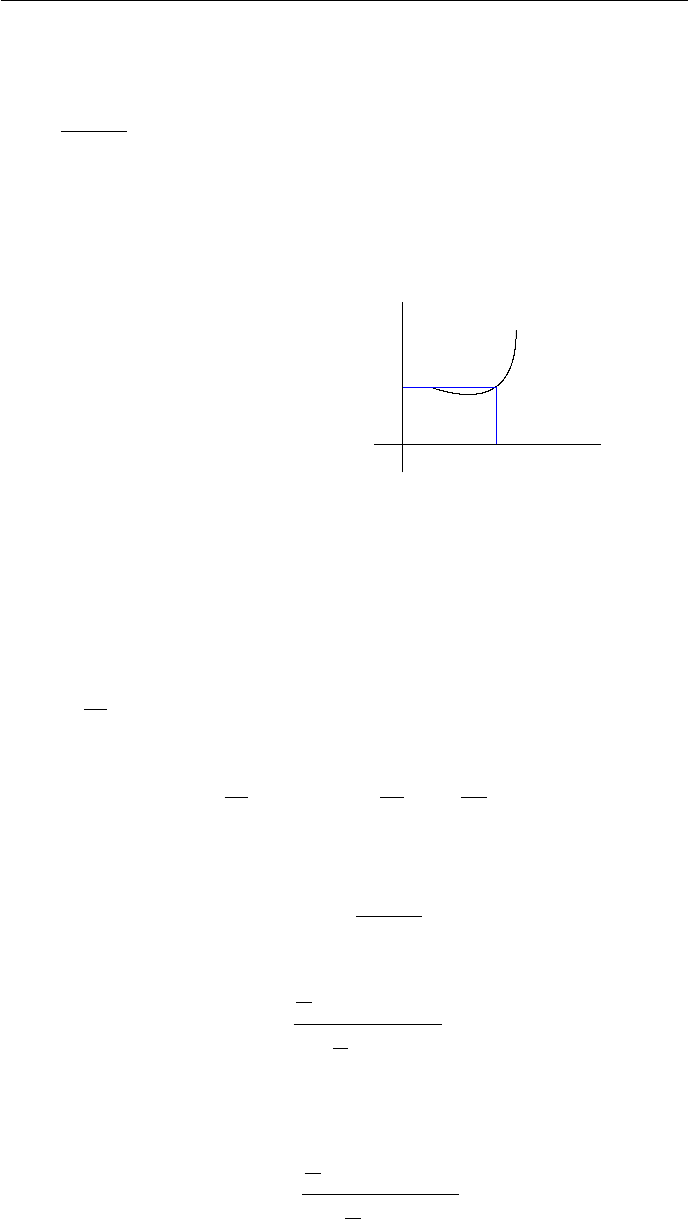
На рис.2.14
показаны функции y = f(x) и
-
6
x
y
,
,
,
,
,
,
e
y = ax + b
y = f (x)
α
Рис. 2.14: Касательная к функции
y = ax+b. Значение a равно tan α и
называется угловым коэффициен-
том. Значение a также равно про-
изводной функции f в точке x
0
: a =
f
0
(x
0
). Тогда y = f
0
(x
0
)∗ x+ b. Точ-
ка касания прямой и функции f (x)
принадлежит этой функции и по-
этому координаты удовлетворяют урав-
нению касательной f(x
0
) = f
0
(x
0
)∗
x
0
+ b. Отсюда
y = f (x
0
) + f
0
(x
0
) ∗ (x − x
0
). (2.16)
или
y = a
0
x + y
0
− a
0
x
0
,
где a
0
=
∂y
∂x
|
x=x
0
.
Попробуем составить соответствие для рисунков 2.13 и 2.14:
a
0
=
∂y
∂x
|
x=x
0
≡ G
0
D
=
I
s
V
T
exp
V
0
D
V
T
,
где G
0
D
и V
0
D
- значения на начальном шаге итерации. Заменив уравнение
2.15 уравнением 2.16 для первого шага итерации получим I
1
D
= G
0
D
V
1
D
+
I
0
D
− G
0
D
V
0
D
, а также, зная, что I
1
D
=
E − V
1
D
R
напряжение на диоде после
первого шага итерации будет равно:
V
1
D
=
E
R
− I
0
D
+ G
0
D
V
0
D
1
R
+ G
0
D
.
Исходя из этого, для схемы, приведённой на рис.2.12, напряжение на
диоде для каждого шага итерации можно выразить как:
V
m+1
D
=
E
R
− I
m
D
+ G
m
D
V
m
D
1
R
+ G
m
D
. (2.17)
17
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
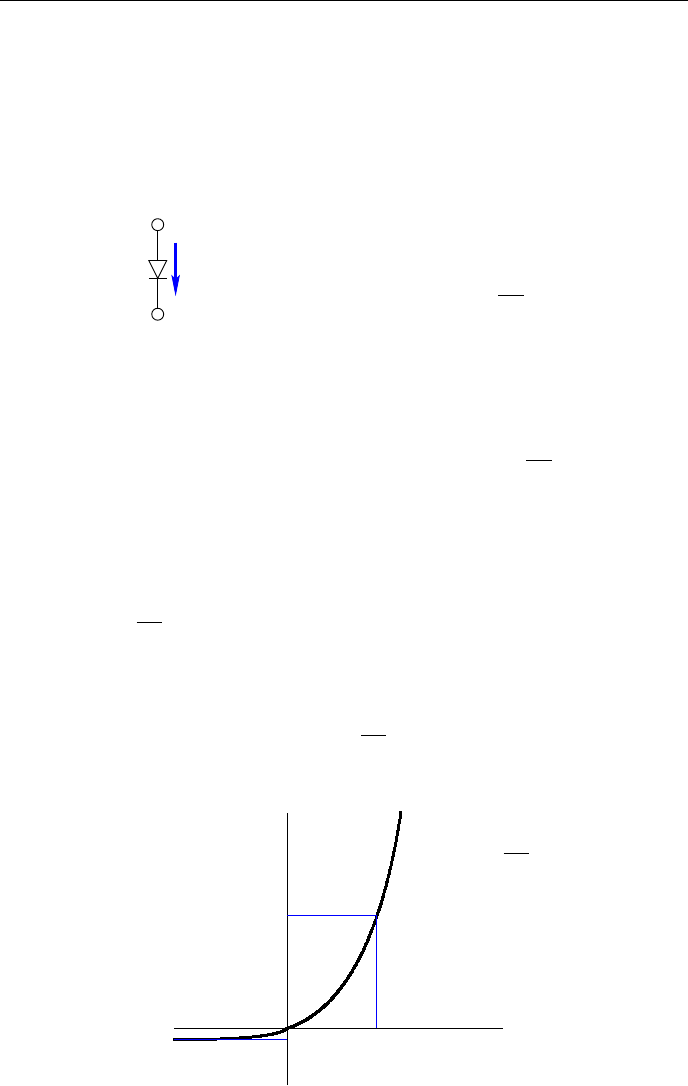
2.7 Диод
Полупроводниковый диод - ниболее распространённый нелинейный эле-
мент. Его изображение
показано на рис.2.15, а вольт-амперная
V
+
−
I
Рис. 2.15: Диод
характеристика (рис.2.16) описывается
уравнением
I = I
s
exp
qV
kT
− 1
, (2.18)
где q = 1.6022 ∗ 10
−19
Кл - заряд
электрона; k = 1.3806 ∗ 10
−23
Дж/К -
постоянная Больцмана; T - температу-
ра в градусах Кельвина; V - напряже-
ние, приложенное к диоду. При 17
◦
C константа V
T
≡
kT
q
' 25mV . Ес-
ли полярность напряжения такая, как показано на рис.2.15, то диод от-
крыт. Ток I
s
- константа, которая зависит от физических свойств диода и
называется током насыщения. Ток принимает значения от 10
−6
до 10
−9
A. Для V < −3V
T
(' 75mV ) I ' −I
s
. Если диод открыт напряжением
V > 4V
T
(более 100mV ), то выражение 2.18 может аппроксимироваться
как I = I
s
exp(
qV
kT
).
Когда к диоду приложено постоянное напряжение V
0
, через него проте-
кает постоянный ток I
0
. Эти величины определяют рабочую точку диода:
I
0
= I
s
exp
V
0
V
T
− 1
. (2.19)
-
6
V
I
I = I
s
(exp(
qV
kT
) − 1)
I
0
V
0
I
s
e
Рис. 2.16: Вольт-амперная характеристика диода
На V
0
могут накладываться малые приращения напряжения, которые
связаны с вариациями тока дифференциальной проводимостью
18
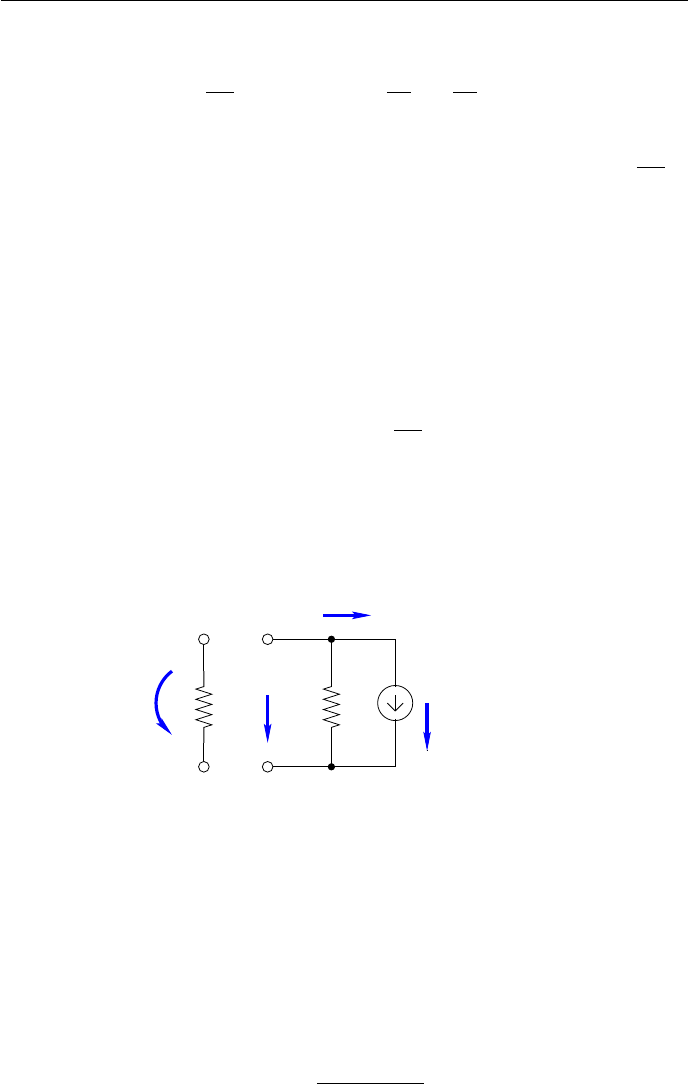
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
∂I
∂V
|
V =V
0
= g(V
0
) =
I
s
V
T
exp
V
0
V
T
, (2.20)
называют динамической проводимостью диода. Величина g(V
0
) =
∂I
∂V
|
V =V
0
равна крутизне характеристики в точке V
0
(рис.2.16).
2.7.1 Нелинейный двухполюсник
На рис.2.17 показан принцип создания нелинейного двухполюсника: ли-
нейная итерационно-замещающая схема нелинейного двухполюсника состо-
ит из параллельного включения омической проводимости G
m
с постоянным
источником тока I
m
− G
m
V
m
, где G
m
=
∂I
∂V
|
V =V
m
- крутизна характери-
стики на m- том шаге итерации, I
m
- ток на m- том шаге итерации, V
m
-
напряжение на m-том шаге итерации.
i=f(u) i
(m+1)
u
(m+1)
i
(m)
−G
(m)
u
(m)
G
(m)
G
(m)
=(di/du)
u
Рис. 2.17: Схема замещения нелинейного двухполюсника
Проводимость G
m
можно определить через отношение разности тока и
напряжения:
G
m
=
I
m+1
− I
m
V
m+1
− V
m
.
Отсюда I
m+1
= G
m
V
m+1
+ I
m
− G
m
V
m
, из которого можно рассчитать
итерационную схему замещения.
Матрица проводимостей и векторных токов показана на следующем ри-
сунке (рис.2.18):
19
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
Схема замещения Матрица проводимостей Матрица токов
G
(m)
(L)
(M)
i
(m)
−G
(m)
u
(m)
L M
L
G
(m)
−G
(m)
M
−G
(m)
G
(m)
L
G
(m)
U
(m)
− I
(m)
M
−G
(m)
U
(m)
+ I
(m)
Рис. 2.18: Матрица проводимостей и векторных токов нелинейного двухпо-
люсника
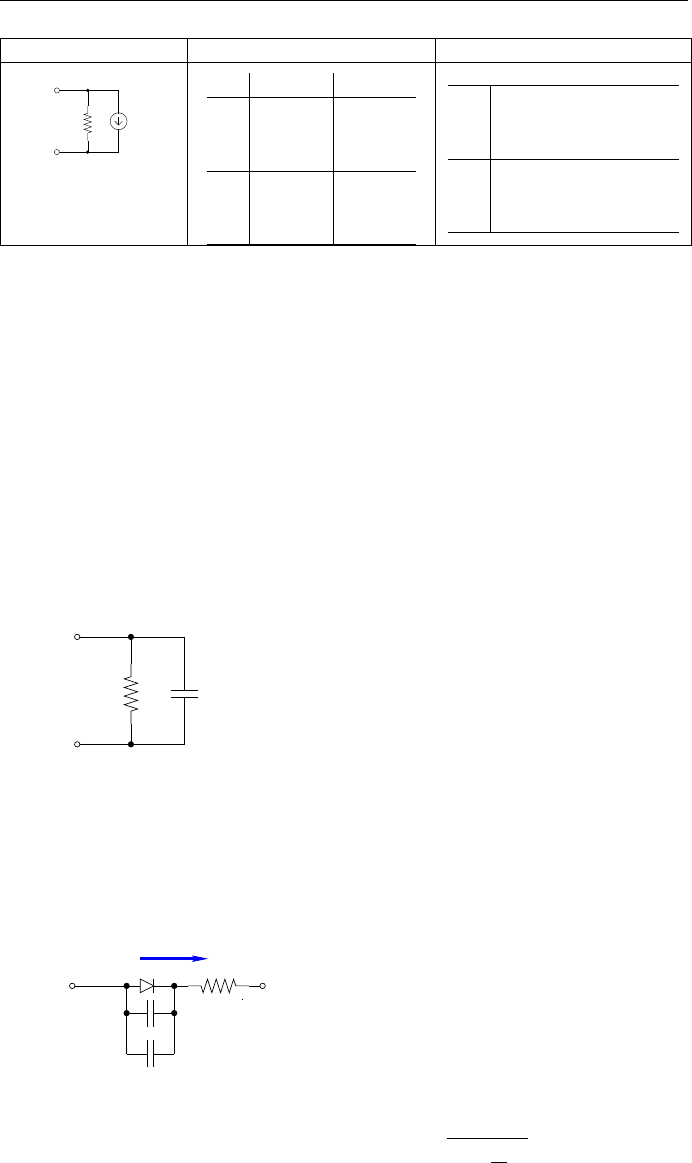
2.7.2 Расширенная модель диода
При переходе к более высоким частотам начинаются сказываться до-
полнительные физические эффекты и диод уже нельзя рассматривать как
нелинейтый резистор. Заряды, накапливаемые в полупроводниковом мате-
риале, вызывают запаздывание напряжения относительно тока.
Для отражения такого эффек-
g(V
0
C(V
0
)
)
Рис. 2.19: Малосигнальная модель ди-
ода на средних частотах
та в эквивалентную схему диода на
малом сигнале параллельно дина-
мической проводимости включают
конденсатор (рис.2.19), ёмкость ко-
торого является функцией напря-
женя в рабочей точке диода.
Для некоторых применений та-
кая простая модель не описывает
достаточно точно свойства диода,
поэтому требуется её модификация.
Одна такая модель с постоянным
сопротивлением R, представляющим
объёмное сопротивление материала, показана на рис 2.20.
В этой модели ёмкость конден-
R
C
d
C
b
I
+ −
Рис. 2.20: Более общая модель диода
сатора, подключенного к диоду, раз-
делена на два компонента: C
b
- ба-
рьерную ёмкость перехода и C
d
-
диффузионную ёмкость. Ёмкость C
b
является функцией напряжения на
диоде и определяется напряжением
C
b
=
C
b
0
(1 −
V
φ
)
γ
для V ≤ φ − Z
K
1
V + K
2
для V > φ − Z
(2.21)
20
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
где
K
1
=
∂C
b
∂V
|
V =φ−Z
; K
2
= −K
1
(φ − Z) + C
b
|
V =φ−Z
.
Значение φ зависит от материала (∼ 0.8V для кремния - Si, ∼ 0.4V для
германия - Ge), а значение γ принимает значение в пределах от 1/2 до 1/3.
Ёмкость C
b
0
обычно составляет несколько пикофарад.
Диффузионная ёмкость C
d
моделируется выражением
C
d
=
(
τ
∂I
∂V
для V > 0
0 для V ≤ 0
(2.22)
где
∂I
∂V
- производная от выражения 2.18, а τ - постоянная, определяемая
экспериментально; C
d
- обычно больше C
b
и может принимать значения в
диапазоне 50 . . . 1000 pF.
2.8 Транзистор
Биполярные транзисторы представляют собой два встречновключенных
взаимодействующих перехода. Взаимодействие переходов происходит черех
тонкую область базы, ширина которой в современых транзисторах состав-
ляет менее 1 мкм. На рис. 2.21
приведены условные обозначения
C
E E
C
BB
n−p−n p−n−p
Рис. 2.21: Биполярные транзисторы
биполярных транзисторов n − p − n
и p − n − p - типа проводимостей.
Упрощённая конструкция транзи-
стора, поясняющая принцип его ра-
боты показана на рис. 2.22. Для тран-
зистора справедливо фундаменталь-
ное соотношение: I
E
= I
B
+I
C
. Мож-
но выделить следующие четыре про-
цесса, происходящих при переносе
носителей заряда от эмиттера к кол-
лектору:
1. Инжекция (впрыскивание) электронов из эмиттера в базу;
2. Диффузия и дрейф электронов в области базы;
3. Рекомбинация электронов в области базы, за счёт чего появляется
базовый ток;
4. Экстракция (втягивание) электронов в область коллектора.
21
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
E B C
− +
−+
Рис. 2.22: Упрощённая конструкция транзистора
Для расчёта схем на биполярных транзисторах используются различные
эквивалентные схемы транзисторов. Одна из схем, снованная на физиче-
ских процессах и называемая Т-образной эквивалентной схемой, показана
на рис.2.23.
C
R
R
R
αΙ ∆Ιc
c
c
b
e
∆Ιb
∆Ιe
Рис. 2.23: Т-образная схема замещения транзистора
На данной схеме обозначены:
• R
e
- сопротивление прямо-смещённого эмиттерно-базового перехода;
• R
b
- объёмное сопротивление области базы;
• R
c
- сопротивление обратно-смещённого коллекторно-базового пере-
хода;
• C
c
- ёмкость обратно-смещённого коллекторно-базового перехода;
22
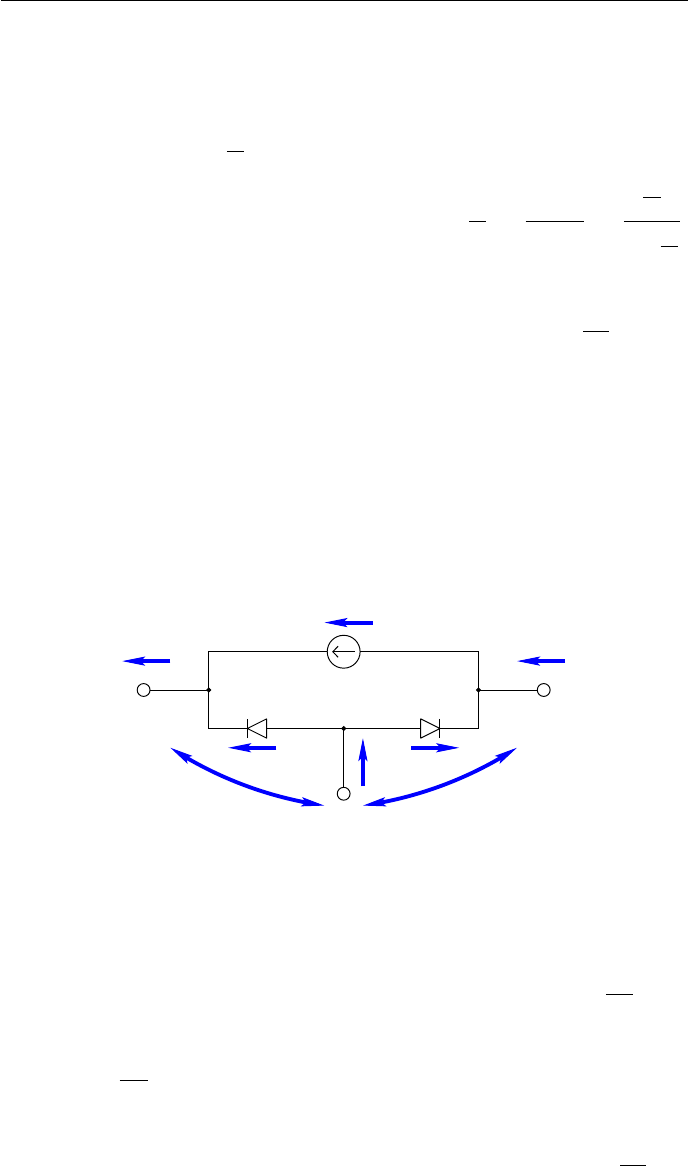
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
• α - коэффициент усиления по току в схеме с общей базой.
Коэффициент усиления по току α для схемы с общей базой рассчиты-
вается по формуле: α =
I
c
I
e
. В схеме с общим эмиттером коэффициент уси-
ления по току рассчитывается по формуле: β =
I
c
I
b
=
I
c
I
e
− I
c
=
I
c
I
e
1 −
I
c
I
e
.
Коэффициент усиления зависит от ьолщины базы. Чем тоньше база, тем
более высокий коэффициент усиления. Сопротивление прямостещённого
эмиттерно-базового перехода определяется по формуле: r
e
=
ϕ
T
I
e
, где ϕ
T
- температурный потенциал, который при нормальной температуре равен
приблизительно 25mV, I
e
- постоянный ток эмиттера.
Однако для расчётов чаще используют более сложную модель замеще-
ния транзистора - модель Эберса-Молла. Существуют несколько разновид-
ностей моделей Эберса-Молла: передаточная модель (рис.2.24), а также бо-
лее сложная, используемая на высоких частотах, модель - с учётом объём-
ных резисторов и нелинейных ёмкостей.
B
U
be
U
bc
Ice
Ie cI
CE
Ici/ Iei/ββ f r
Ib
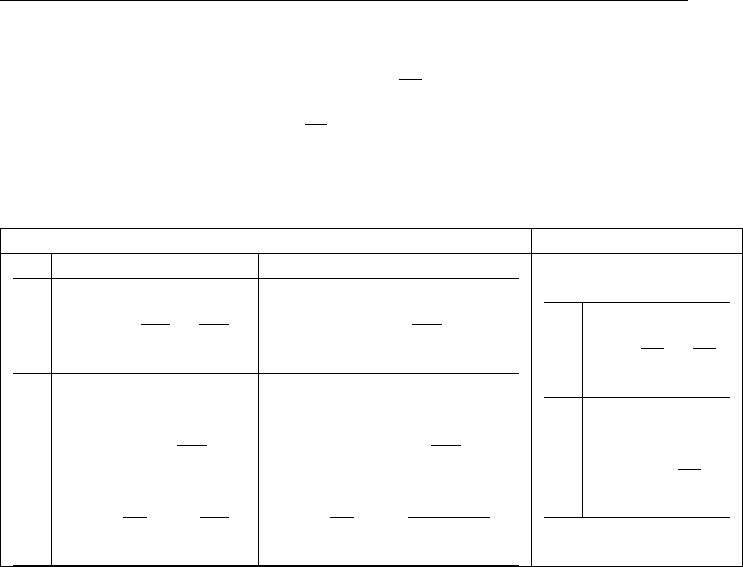
Рис. 2.24: Модель Эберса-Молла
Для данной модели (рис.2.24) I
ce
= I
ci
− I
ei
, где I
ci
= I
s
e
V
be
V
T
− 1
и I
ei
= I
s
e
V
bk
V
T
− 1
- коллекторный (прямой) и эмиттерный (обратный)
источники тока передачи соответственно, I
s
- ток насыщения, V
T
=
kT
q
. Та-
кую модель также называют нелинейной гибридной П-моделью. Токи кол-
лектора и эмиттера равны соответственно:
23
ГЛАВА 2. МОДЕЛИ КОМПОНЕНТОВ
I
c
= (I
ci
− I
ei
) −
I
ei
β
r
I
e
= −
I
ci
β
f
− (I
ci
− I
ei
)
. (2.23)
Ниже приводится таблица матрицы проводимостей и матрицы вектор-
ных токов:
Матрица проводимостей Матрица токов
B C
B
G
11
=
G
ci
β
f
+
G
ei
β
r
G
12
= −
G
ei
β
r
C
G
21
= G
ci
−
−
G
ei
+
G
ei
β
r
G
22
=
G
ei
+
G
ei
β
r
G
ci
=
I
s
V
T
exp
U
be
V
T
G
ei
=
I
s
V
T
exp
U
be
− U
ce
V
T
B
I
e
=
I
ci
β
f
+
I
ei
β
r
C
I
c
= I
ci
−
−
I
ei
+
I
ei
β
r
Таблица 2.6: Матрица узловых напряжений и токов для n−p−n транзистора
Рассмотренные модели пригодны только для низких частот, так как они
не учитывают зарядов, накопленных в полупроводниковом материале.
24

Глава 3
Системы линейных
уравнений
Решение системы линейных уравнений
Для решения системы линейных уравнений существует несколько мето-
дов [2].
3.1 Алгоритм Гаусса
Алгоритм Гаусса также называется методом исключений. Пусть имеется
система линейных уравнений
Ax = b, (3.1)
где A - матрица размера (n ∗ n) с постоянными коэффициентами; b - n-
мерный вектор известных констант и x- n-мерный вектор неизвестных:
a
11
a
12
· · · a
1n
a
21
a
22
· · · a
2n
.
.
.
.
.
.
a
n1
a
n2
· · · a
nn
x
1
x
2
.
.
.
x
n
=
b
1
b
2
.
.
.
b
n
. (3.2)
Формально эту систему уравнений можно решить, обратив матрицу A:
x = A
−1
b. (3.3)
Когда требуется найти только одну “выходную” переменную, исполь-
зуют метод, называемый правилом Крамера. Это правило гласит, что для
системы (3.1) k-я компонента x
k
вектора x равна отношению определителя
матрицы A , в которой k-й столбец заменён вектором b, и определителя
матрицы A:
x
k
=
det(A
k
)
det(A)
. (3.4)
25

ГЛАВА 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Правило Крамера используется для решения уравнений низкого порядка
и при теоретических исследованиях. Этот метод требует больших затрат
машинного времени и редко применяетя в вычислительных программах.
Численное решение систем линейных уравнений часто базируется на ме-
тоде исключений Гаусса. Он основываетия на том факте, что сложение од-
ного уравнения системы с другим, возможно умноженным на константу, не
изменяет решения системы.
Перепишем матричное уравнение (3.2) в координатной форме:
a
11
x
1
+ a
12
x
2
+ · · · + a
1n
x
n
= b
1
a
21
x
1
+ a
22
x
2
+ · · · + a
2n
x
n
= b
2
· · · · · · + · · · · · · + · · · + · · · · · · = · · ·
a
n1
x
1
+ a
n2
x
2
+ · · · + a
nn
x
n
= b
n
(3.5)
Разделим первое уравнение на a
11
и запишем его:
x
1
+ a
(1)
12
x
2
+ a
1)
13
x
3
+ · · · = b
(1)
1
,
где a
(1)
12
=
a
12
a
11
, и т.д. Умножим это уравнение на −a
21
и сложим его со
вторым уравнением. Коэффициенты вновь полученного второго уравнения
a
(1)
2j
= a
2j
− a
21
a
(1)
1j
, j = 1, 2, . . . , n + 1. Такой выбор множителя обеспечива-
ет равенство нулю коэффициента a
(1)
21
. Аналогично для других уравнений
подстановка
a
(1)
ij
= a
ij
− a
i1
a
(1)
1j
,
i = 2, 3, . . . , n,
j = 1, 2, . . . , n + 1,
обеспечивает равенство нулю всех коэффициентов в первом столбце мат-
рицы A, за исключением a
(1)
11
, который равен 1. В результате этих операций
уравнения примут вид:
x
1
+ a
(1)
12
x
2
+ a
(1)
13
x
3
+ · · · + a
(1)
1n
x
n
= b
(1)
1
a
(1)
22
x
2
+ a
(1)
23
x
3
+ · · · + a
(1)
2n
x
n
= b
(1)
2
· · · · · · + · · · · · · + · · · + · · · · · · = · · ·
a
(1)
n2
x
2
+ a
(1)
n3
x
3
+ · · · + a
(1)
nn
x
n
= b
(1)
n
.
Индекс в скобках показывает, что коэффициенты были один раз изме-
нены. На следующем шаге исключается из рассмотрения первые строка
и столбец. Аналогично надо выполнить ранее описанные процедуры для
уравнений от второго до n-го.
Исключение по Гауссу требует выполнения ∼
n
3
3
, где n- порядок матри-
цы, а обратная подстановка может быть выполнена приблизительно за
n
2
2
операций.
Ниже приводится пример программы расчёта системы линейных урав-
нений методом Гаусса, написанный на языке Паскаль (4.5).
3.2 Другие методы
26

ГЛАВА 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
Кроме метода Гаусса существуют и другие методы решения системных
уравнений, например метод Гаусса с выбором главного элемента, заклю-
чающийся в том, что при прямом ходе производится выбор наибольшего по
модулю (главного) элемента и перестановка строк или столбцов. Последнее
исключает деление на ноль, если матрица содержит нулевые элементы, и
повышает точность вычислений при наличии ошибок округления.
Разновидностью метода Гаусса является и метод вращения, обладаю-
щий повышенной устойчивостью к “провалам” промежуточных вычисле-
ний. Этот метод обеспечивает приведение исходной системы к системе с
правой треугольной матрицей.
Метод LU-разложения. Лучшим методом решения системы линейных
уравнений является метод разложения на треугольные матрицы, или ме-
тод LU-факторизации. Алгоритмы этого метода близки к методу исклю-
чения Гаусса, хотя вычисления могут проводиться в различной последо-
вательности. Главным преимуществом методом LU-факторизации в срав-
нении с методом исключения Гаусса является возможность более простого
получения решений для различных векторов b в правой части системы
(3.1), а также для транспонированной системы уравнений, что требуется
при расчёте чувствительностей.
27

ГЛАВА 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
28
Глава 4
Приложение
4.1 Основы операций с матрицами
4.1.1 Матрицы и детерминанты
Матрицей размеров m ∗ n называется прямоугольная таблица чисел, со-
держащая m строк и n столбцов. Числа, составляющие матрицу, называют-
ся элементами матрицы. Обычно принято обозначать матрицы большими
буквами, а саму таблицу чисел заключать в скобки (круглые, прямоуголь-
ные или двойные прямые линии). Например, A =
1 3 −2
4 −5 6
- матрица
размеров 2 ∗ 3, B =
0
0
0
- матрица размеров 3 ∗ 1, или другими словами,
матрица-столбец.
Для обозначения элементов матрицы используется та же буква, что и
для самой матрицы, только маленькая, напр.:
A =
a
11
a
12
· · · a
1n
a
21
a
22
· · · a
2n
.
.
.
.
.
.
a
m1
a
m2
· · · a
mn
(4.1)
В этой записи a
ij
означает, что элемент находится в строке с
номером i и столбце с номером j.
Определитель, или детерминант, квадратной матрицы с n
2
(действительными или комплексными) числами (элементами) a
ik
есть сумма n! членов (−1)
r
a
1k
1
a
2k
2
. . . a
nk
n
, каждый из которых
соответствует одному из n! различных упорядоченных множеств
k
1
, k
2
, . . . , k
n
, полученных r попарными перестановками (транс-
позициями) элементов из множества 1, 2, . . . , n. Число n есть по-
рядок определителя.
Пример вычисления определителей второго и третьего поряд-
ка:
29

ГЛАВА 4. ПРИЛОЖЕНИЕ
a
11
a
12
a
21
a
22
= a
11
a
22
− a
12
a
21
(4.2)
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
=
a
11
a
22
a
23
a
32
a
33
− a
12
a
21
a
23
a
31
a
33
+ a
13
a
21
a
22
a
31
a
32
=
a
11
a
22
a
23
a
32
a
33
− a
21
a
12
a
13
a
32
a
33
+ a
31
a
12
a
13
a
22
a
23
.
(4.3)
4.1.2 Сложение и вычитание
Сложение определено только для матриц одинаковых размеров. Суммой
матриц A и B размером m ∗ n является матрица C таких же размеров, у
которой c
ij
= a
ij
+ b
ij
, i = 1, 2, ..., m, j = 1, 2, ..., n.
Операцию вычитания матриц можно определить следующи м образом:
A − B = A + (−1)B, что соответствует вычитанию элементов, стоящих на
одинаковых местах.
4.1.3 Умножение
Произведением матрицы A размеров m ∗ n на число α называется мат-
рица C таких же размеров, у которой c
ij
= αa
ij
, i = 1, 2, ..., m, j = 1, 2, ..., n.
Другими словами, при умножении матрицы на число все её элементы умно-
жаются на это число.
Произведение матрицы A размером m ∗ n на матрицу B размером n ∗ k
называется матрица C размером m ∗ k , элементы которой вычисляются по
формуле:
c
ij
= a
i1
b
1j
+ a
i2
b
2j
+ ... + a
in
b
nj
=
n
X
s=1
a
is
b
sj
(4.4)
где i = 1, 2, ..., m, j = 1, 2, ..., k.
1
4.2 Основы теории графов
4.2.1 Основные понятия
1
В этом определении надо обратить вни мание на порядок сомножителей! Произведе-
ние определено только тогда, когда число столбцов первого сомножителя равно числу
строк второго! Размеры результата умножения определяются следующим образом: число
строк результата должно быть равно числу строк первого сомножителя, а число столбцов
результата равно числу столбцов второго сомножителя.
30

ГЛАВА 4. ПРИЛОЖЕНИЕ
Граф - это схематическое изображение некоторого множества элементов
и взаимосвязей. Графы характеризуют какое-то определённое состояние си-
стемы (напр. электрических цепей). Граф в общем случае состоит из вер-
шин (узлов) - условных изображений составляющих его элементов и рёбер
(ветвей) - линий, соединяющих все или некоторые эти вершины. Вершины,
соединённые ребром, называют смежными. Рёбра, имеющие определёное
направление, указывающие на порядок взаимодействия вершин, называют-
ся ориентироанными рёбрами. Они изображаются стрелками.
Одно из важнейших достоинств графов заключается в том, что часто
удаётся отказаться как от составления эквивалентных схем, так и от записи
управлений для их анализа.
Направленным графом называют конфигурацию, состоящую из точек
или вершин (узлов) и ориентированных линий (ветвей), соединяющих эти
точки.
4.2.2 Решение графа
Решить граф - это значит найти связь между его двумя любыми пере-
менными.
Существуют два способа решения. Один из них опирается на топологи-
ческие свойства графа и состоит в том, что сложный граф путём последова-
тельных операций упрощается до одной ветви. Передача этой ветви равна
передаче графа. Эти преобразования эквивалентны исключению лишних
переменных из системы уравнений.
Второй путь позволяет получить ответ непосредственно из исходного
графа. В этом случае решение записывается сразу в виде формулы Ме-
зона [5]. но такой путь решения может оказаться не столь эффективным.
В процессе последовательных упрощений графа удаётся наглядно оценить
роль того или иного параметра в конечном результате, подметить наличие
скрытых обратных связей, оценить степень их влияния и т. д.
4.2.3 Правила преобразования графов
Ниже приводятся некоторые правила с графами:
31
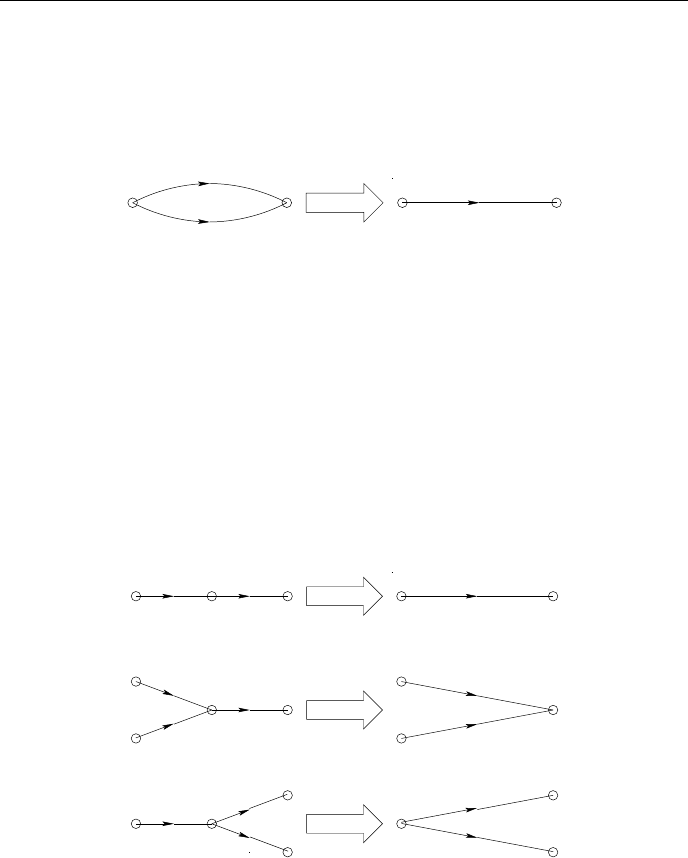
ГЛАВА 4. ПРИЛОЖЕНИЕ
x1
a
b
x2
a+b
x1 x2
x2=(a+b)*x1
Рис. 4.1: Сложение с исключением ветви
x1 x1
a b
x2 x3
x1
x2
x3 x4
a
b
c
x1
x2
x4
ac
bc
x1 x2
x3
x4
x1
x4
x3a
b
c
ab
ac
x2=a*x1 x3=b*x2
x3x3=ab*x1
x3=a*x1+b*x2
x4=c*x3
x4=ac*x1+bc*x2
x2=a*x1;x3=b*x2;x4=c*x2 x3=ab*x1;x4=ac*x1
Рис. 4.2: Умножение с исключением узла
Исключение контура обратной связи
Рассмотрим случай, когда контур обратной связи является петлёй (рис.4.3):
32

ГЛАВА 4. ПРИЛОЖЕНИЕ
x1 x2 x1 x2
b
a a/(1−b)
Рис. 4.3: Исключение петли
для графа сигнал x
2
определяется из уравнения x
2
= ax
1
+ bx
2
. Решая
уравнение относительно x
2
получим: x
2
=
a
1 − b
x
1
. Отсюда следует прави-
ло:
Для того, чтобы исключить петлю, необходимо передачу a-ветви,
входящую в узел с петлёй b, заменить передачей
a
1 − b
.
Если в смешанный узел входит и выходит из него несколько ветвей,
то правило ликвидации петли применяется для каждой входящей
ветви. Передачи выходных ветвей не изменяются.
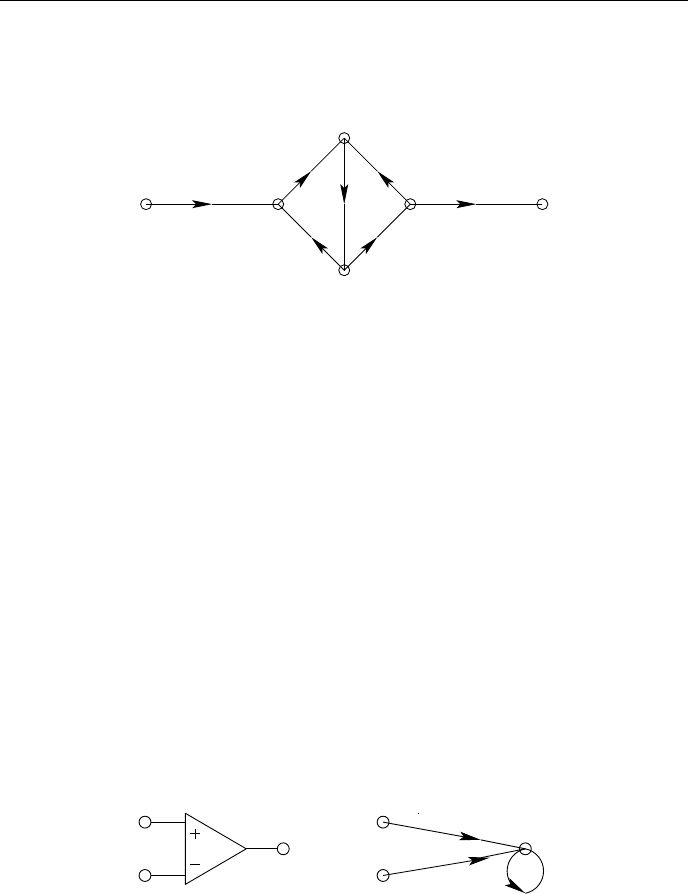
4.2.4 Примеры с графами
Попробуем нарисовать граф схемы, показанной на рис.4.7. Для этого
вначале составим уравнения:
U
2
= I
3
R
4
I
1
=
E − U
1
R
1
U
1
= I
2
R
2
I
2
= I
1
− I
3
I
3
=
U
1
R
3
+ R
4
.
Граф, воспроизводящий эту схему, выглядит так:
33
ГЛАВА 4. ПРИЛОЖЕНИЕ
E
1/R1
1
I2
U1
I1 I3
1/R1 1/(R3+R4)
R4
−1
R2
Рис. 4.4: Граф схемы (рис.4.7).
Приведённая форма графа является не единственной и может быть пре-
образована в другую, применяя правила графов.
В качестве примера рассмотрим ещё граф операционного усилителя ОУ
и граф схемы ОУ с отрицательной обратной связью. В большинстве случа-
ев при расчёте схем с ОУ допустима идеализация параметров последнего.
Обычно принимают R
in
→ ∞ и R
out
→ 0, а усиление K
0
в рабочей поло-
се частот неизменным. При такой идеализации граф ОУ может выглядеть
так:
1
2
3K
1
2
3
G
KG
−KG
Рис. 4.5: ОУ и его граф
Собственные проводимости входов 1 и 2 равны нулю (теоретически) и
поэтому не изображаются, а собственная выходная проводимость G в графе
сохраняется. Если G → ∞, то при любой нагрузке усилителя (любой про-
водимости, добавляемой к G) усиление ОУ должно сохранять неизменную
величину, равную K
0
. Этот результат можно получить, образуя из графа
34
ГЛАВА 4. ПРИЛОЖЕНИЕ
проводимостей граф сигнала, только в том случае, если взаимная проводи-
мость равна K
0
G. Обратная взаимная проводимость принимается равной
нулю и на графе не изображается (в самом усилителе отсутствует паразит-
ная обратная связь с выхода на вход). На рис.4.6 изображена схема инвер-
тирующего ОУ и его граф, построенный по правилу Мезона.
UIN
(1) (2)
G1 G2
GL
UOUT
G1
G1+G2
G2
−K0*G+GL
(3)
(3)
(2)
(1)
α
β
K
G2+GL+G
Рис. 4.6: Усилитель на ОУ
Для данной схемы имеем: α =
G
1
G
1
+ G
2
, β =
G
2
G
1
+ G
2
, K =
−K
0
G
1
+ G
2
G + G
2
+ G
L
'
(−K
0
) |
k
0
→∞
. Тогда U
OU T
= U
IN
−αK
0
1 + βK
0
' −
α
β
=
G
1
G
2
.
4.3 Законы Кирхгофа
Первый закон Кирхгофа. Алгебраическая сумма токов, протекающих че-
рез узел, равна нулю:
I =
n
X
j=1
I
j
= 0 (4.5)
Узлом в электрической цепи называеися место соединения трёх и более
ветвей. Ток берётся со знаком плюс, если ток втекает в узел, и со знаком
минус, если вытекает.
Ветвью называется участок цепи с последовательным соединением эле-
ментов.
Второй закон Кирхгофа. Алгебраическая сумма падений напряжений
вдоль любого замкнутого контура электрической цепи равна нулю:
E
Σ
=
n
X
j=1
±U
j
= 0. (4.6)
35

ГЛАВА 4. ПРИЛОЖЕНИЕ
Или, алгебраическя сумма ЭДС всех источников в любом замкнутом
контуре цепи равна алгебраической сумме напряжений на всех остальных
элементах того же контура
2
.
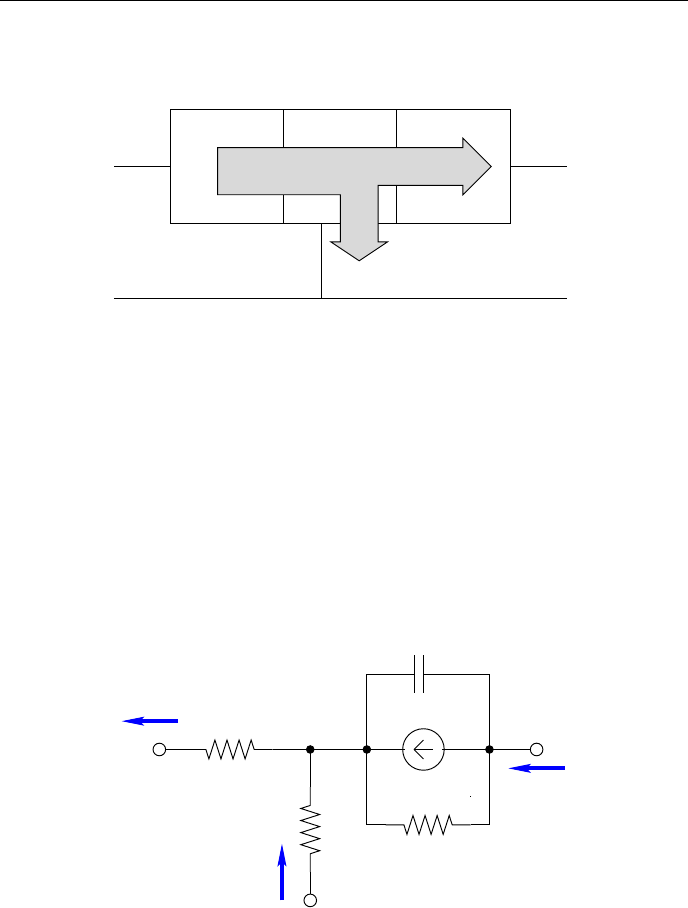
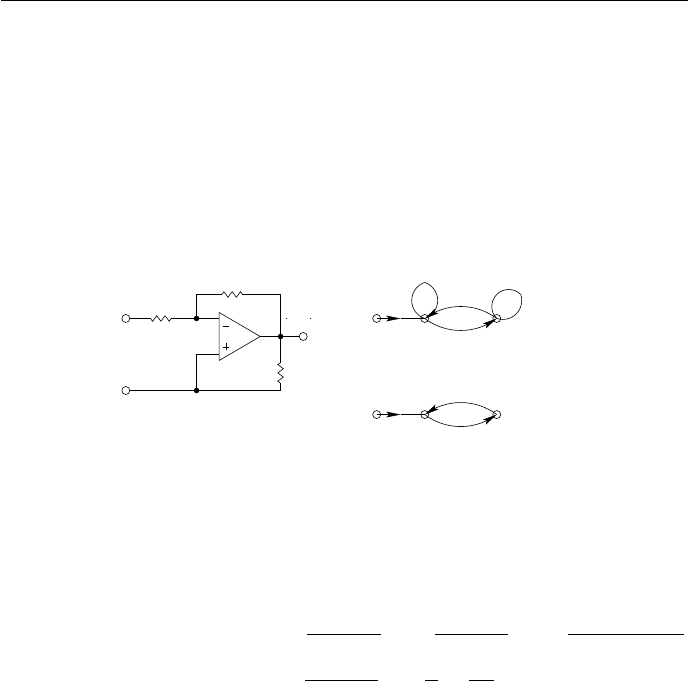
4.3.1 Метод узловых потенциалов
Метод узловых потенциалов, или метод узловых напряжений, один из
общих методов расчёта режима в линейных электрических цепях (то есть
метод определения токов во всех ветвях цепи и напряжений на зажимах
всех приёмников и источников электрической энергии), при котором за
неизвестные величины принимают потенциалы узлов схемы. Исходными
для расчёта цепи величинами являются входные сопротивления (или про-
водимости) приёмников и внутренние сопротивления (проводимости) и эдс
(или токи) источников. Для всех узлов, кроме одного (базового), потенци-
ал которого обычно выбирается равным нулю, составляются уравнения в
соответствии с первым законом Кирхгофа (см. правила Кирхгофа), причём
каждый из неизвестных токов выражается через сопротивления, эдс и по-
тенциалы узлов согласно обобщённому закону Ома. Из полученной системы
n − 1 независимых уравнений (где n - число узлов схемы) определяются по-
тенциалы узлов (равные напряжениям между каждым из узлов и базовым),
а затем (по закону Ома) токи ветвей и напряжения на зажимах приемников
и источников. Если заданы напряжения между какими-либо парами узлов
или известны токи в некоторых ветвях, то число независимых уравнений
меньше n − 1. Уравнения можно записать и решать в матричной форме.
Этот метод даёт более простое решение задачи, чем метод контурных токов,
обычно в тех случаях, когда с использованием метода узловых потенциалов
получается меньшее число независимых уравнений.
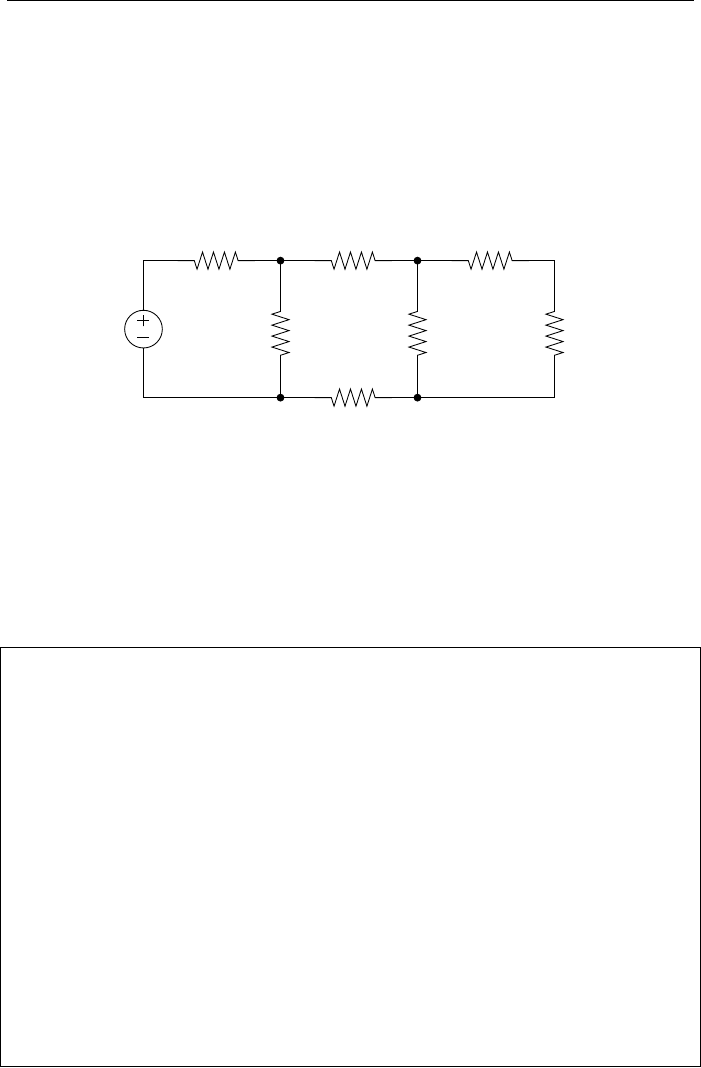
4.3.2 Метод контурных токов
Метод контурных токов - это метод расчёта электрических цепей, при
котором за неизвестные принимаются токи в контурах, образованных неко-
торым условным делением электрической цепи:
Например, в электрической це-
E
R1
R2
R3
R4
I1 I3
I2
U2
I II
U1
Рис. 4.7: Контурные токи
пи выделены контуры I и II и обо-
значены контурные токи i
1
и i
2
, на-
правленные по часовой стрелке. В
соответствии со вторым правилом
Кирхгофа система уравнений, за-
писанная для контурных токов, бу-
дет выглядеть так:
(
R
1
i
1
+ R
2
i
1
− R
2
i
2
= E(для контура I);
−R
2
i
1
+ R
2
i
2
+ R
4
i
2
= 0(для контура I).
(4.7)
2
Примечание: знак + выбирается перед падением напряжения на резисторе, если на-
правление протекания тока через него и направление обхода контура совпадают; для
падений напряжения на источниках ЭДС знак + выбирается, если направление обхода
контура и направление действия ЭДС встречны независимо от направления протекания
тока.
36
ГЛАВА 4. ПРИЛОЖЕНИЕ
4.4 Примеры описания электрических схем
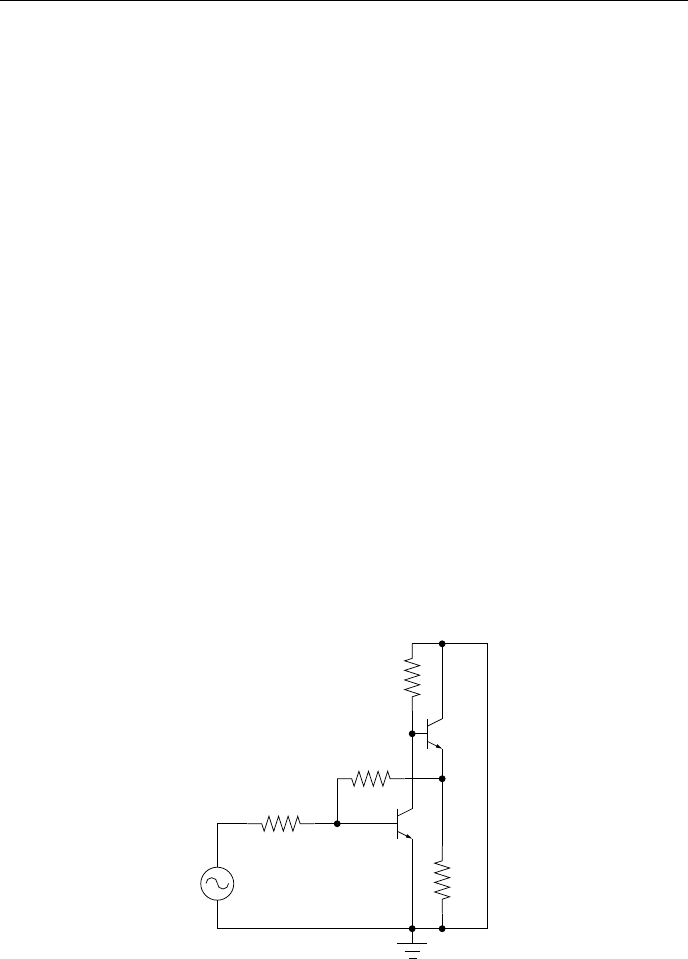
4.4.1 Пример схемы с резисторами
R
R
R
R
R R
R
(1)
(0) (4)
(2) (3)
E
1
3
1
in 2 5
4
6
Рис. 4.8: Пример схемы с описанием
Описание схемы (рис.4.8) может выглядеть так:
{*}
{*} Sample
{*}
{*} Type Node1 Node2 Nominal
{*}
R1 0 1 24 K
R2 1 2 4K
R3 0 4 2K
R4 2 4 10 K
R5 2 3 6K
R6 3 4 9K
{*}
{*} Element Type Node (+) Node ( -) Nominal Nominal
{*}
E1 0 1 0 22.5 7K
Матрица A для такой схемы будет выглядеть так:
G
1
+ G
3
+ G
in
−G
1
− G
in
0 0 −G
3
−G
1
− G
in
G
1
+ G
2
+ G
in
−G
2
0 0
0 −G
2
G
2
+ G
4
+ G
5
−G
5
−G
4
0 0 −G
5
G
5
+ G
6
−G
6
−G
3
0 −G
4
−G
6
G
3
+ G
4
+ G
6
37
ГЛАВА 4. ПРИЛОЖЕНИЕ
Матрица b будет выглядеть так:
−EG
in
EG
in
0
0
0
После решения системы уравнений результат будет такой:
x
0
' −9.1, x
1
' 3, x
2
' −1.05, x
3
' −3.5, x
4
' −7.1.
Чтобы узнать напряжение в узлах относительно нулевого узла, надо
произвести вычитание значений результатов интересующенго узла и нулево-
го узла, например напряжение в узле (1) будет равно: U
1,0
= x
1
− x
0
= 12.1.
4.4.2 Пример с использованием источников тока, управ-
ляемых напряжением
Для примера будет взят n − p − n - транзистор SF − 225 со следующими
характеристиками:
U
ce
= 10V, I
c
= 1mA, f = 450kGz. Матрица проводимостей будет: g
11
=
0.2mS, g
12
= 0, g
21
= S = 30mS, g
22
= 0.0.1mS.
Схема приведениа на следующем рисунке (рис. 4.9):
1mv
1k
100k
1k
1k
Q1
Q2
Рис. 4.9: Схема транзисторного усилителя
Схема замещения для данной схемы будет выглядеть так (рис. 4.10):
Для матрицы A коэффициенты будут такими:
a
1,1
= g
i
+ g
1
+ g
7
; a
1,2
= 0; a
1,3
= −g
7
; a
1,0
= −g
i
− g
1
;
a
2,1
= S
q1
; a
2,2
= g
2
+ g
3
+ g
4
; a
2,3
= −g
4
; a
2,0
= −S
q1
− g
2
− g
3
;
a
3,1
= −g
7
; a
3,2
= S
q2
− g
4
; a
3,3
= −S
q2
+ g
4
+ g
5
+ g
6
+ g
7
; a
3,0
= −g
5
− g
6
;
a
0,1
= S − g
i
− g
1
; a
0,2
= −g
2
− g
3
; a
0,3
= S − g
5
− g
6
; a
0,0
= −S + g
i
+ g
1
+
g
2
+ g
3
+ g
4
+ g
5
+ g
6
.
38
ГЛАВА 4. ПРИЛОЖЕНИЕ
1mv
1k
5k
1k
100k 5k
1k
100k
S=30mA/V
100k
S=30mA/V
g
g
g
g
(3)
(0)
(1) (2)
−
+
−
+
+
−
+
−
g
i
1
5
4
2
g
7
6
g
g
3
Рис. 4.10: Схема замещения транзисторного усилителя
Для матрицы b коэффициенты равны:
b
1
= Eg
i
; b
2
= 0; b
3
= 0; b
0
= −Eg
i
.
В результате напряжения в точках 1, 2, 3 относительно точки 0 будут
равны:
x
1,0
' 0.00065; x
2,0
' −0.01969; x
3,0
' −0.02039.
4.4.3 Пример о операционным усилителем
В качестве примера возьмем схему инвертирующего усилителя и соста-
вим матрицы проводимости A и токов b (см. рис.4.11):
−
−
+
+
R1 100K
Ri 1K
E1
1mV
Ro 0.01
(2)
(1)
(0)
S=1E7
Рис. 4.11: Инвентирующий операционный усилитель
39

ГЛАВА 4. ПРИЛОЖЕНИЕ
Матрица проводимостей A будет равна:
(g
i
+ g
1
) −g
1
−g
i
(−g
1
+ S) (g
1
+ g
o
) (−g
o
− S)
(−g
i
− S) −g
o
(g
i
+ g
o
+ S)
,
а матрица токов b :
Eg
i
0
−Eg
i
.
После решения системы уравнений получим значения в точках (1, 2)
относительно точки (0):
u
1,0
= 0.0001; u
2,0
= −9.9989.
4.5 Листинги программ
4.5.1 Гаусс
program gauss ;
const nn =1000;
var
a : array [1.. nn ,1.. nn ] of double ;
x ,b : array [1.. nn ] of double ;
n ,i,j ,k : integer ;
d : double ;
begin
write (’ Enter n : ’) ;
read ( n);
for i :=1 to n do
begin
for j :=1 to n do
begin
write (’a [’, i:3 ,’ ,’ ,j :3 , ’]: ’);
read (a [i, j]) ;
end ;
end ;
for i :=1 to n do
begin
write (’b [’, i :3 , ’]: ’) ;
read (b [i ]) ;
end ;
for i :=1 to n -1 do
begin
for k := i +1 to n do
begin
d := a[k ,i ]/ a[i ,i ];
for j := i +1 to n do
40

ГЛАВА 4. ПРИЛОЖЕНИЕ
a[k ,j ]:= a[k ,j] -a[i ,j ]* d;
b[ k ]:= b[ k]- b[i ]* d;
end ;
end ;
for i := n downto 1 do
begin
for j := i +1 to n do
b[ i ]:= b[ i]- a[i , j ]* x[j ];
x[ i ]:= b[ i]/ a[i , i ];
end ;
for i :=1 to n do
writeln ( ’x[ ’,i :3 , ’]= ’ ,x [ i ]:1:5) ;
end .
41

ГЛАВА 4. ПРИЛОЖЕНИЕ
42
Литература
[1] F¨uhrer A., Hedemann K., Nerreter W. Grundgebiete der Elektrotechnik. 2.
Bande. M¨unchen, 1986.
[2] Kremer H. Numerische Berechnung Linearer Netzwerke und Systeme. Berlin,
1978.
[3] Calahan D. Computer-Aided Network design. New-York, 1972.
[4] Katzenelson J. An algorithm for solving nonlinear resistive networks. Bell
Syst. Tech. J., Vol 44, pp. 1605-1620, October 1965.
[5] Мезон С., Циммерман Г. Электронные цепи, сигналы и системы. М.,
Изд-во иностр. лит., 1963. 620 с. с ил.
[6] Мамонкин И. Г. Электронные устройства. Учебное пособие для вузов.
Изд. 2-е, доп. и перераб. М., “Связь”, 1977.
43